题目内容
用黑白两种正六边形地面瓷砖按如图所示规律拼成若干图案,则第8个图案中有白色地面瓷砖 块.


考点:规律型:图形的变化类
专题:
分析:根据第1个图形有6块白色地面瓷砖,第2个图形有10块白色瓷砖,每多1个黑色瓷砖则多4块白色瓷砖,根据此规律即可写出第n个图案中的白色瓷砖的块数.
解答:解:第1个图案白色瓷砖的块数是:6,
第2个图案白色瓷砖的块数是:10=6+4,
第3个图案白色瓷砖的块数是:14=6+4×2,
…
以此类推,第n个图案白色瓷砖的块数是:6+4(n-1)=4n+2.
当n=8时,4n+2=4×8+2=34,
故答案为:34.
第2个图案白色瓷砖的块数是:10=6+4,
第3个图案白色瓷砖的块数是:14=6+4×2,
…
以此类推,第n个图案白色瓷砖的块数是:6+4(n-1)=4n+2.
当n=8时,4n+2=4×8+2=34,
故答案为:34.
点评:本题考查了图形的变化问题的规律探寻,看出图形变化规律“每多一块黑色瓷砖则白色瓷砖增加4块”是解题的关键.

练习册系列答案
相关题目
无论取何值时,抛物线y=a(x+k)2+k的顶点总在( )
| A、x轴上 | B、y轴上 |
| C、直线y=-x上 | D、直线y=x上 |
把抛物线y=x2-3x+5的图象向左平移3个单位,再向上平移2个单位得到图象的解析式,则有( )
| A、b=3,c=7 |
| B、b=9,c=-15 |
| C、b=-3,c=-2 |
| D、b=-9,c=21 |
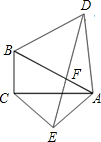 如图,已知在直角三角形ABC中,∠BCA=90°,
如图,已知在直角三角形ABC中,∠BCA=90°, △ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB、AC于E、F.且BE=EO.
△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作一直线交AB、AC于E、F.且BE=EO.