题目内容
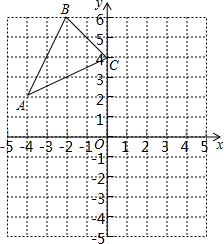 如图,在平面直角坐标系中,O是坐标原点,A、B、C的坐标分别是(-4,2),(-2,6),(0,4),点D是AB边上任意一点.
如图,在平面直角坐标系中,O是坐标原点,A、B、C的坐标分别是(-4,2),(-2,6),(0,4),点D是AB边上任意一点.(1)若点D的坐标是(m,n),D′的坐标(m+4,n-1),平移△ABC至△A′B′C′,使点D与点D′重合,画出平移后的图形,并写出点A的对应点A′的坐标;
(2)将△ABC绕点O逆时针旋转90°,得到△A1B1C1,画出△A1B1C1;
(3)以图中的点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
考点:作图-位似变换,作图-平移变换,作图-旋转变换
专题:
分析:(1)根据题意得出平移△ABC至△A′B′C′,是向右平移4个单位,再向下平移1个单位得到,进而得出△A′B′C′的位置;
(2)利用旋转变换的性质得出对应点位置进而得出答案;
(3)利用位似变换的性质,进而得出对应点位置即可得出答案.
(2)利用旋转变换的性质得出对应点位置进而得出答案;
(3)利用位似变换的性质,进而得出对应点位置即可得出答案.
解答: 解:(1)如图所示:△A′B′C′即为所求,A′的坐标为:(0,1);
解:(1)如图所示:△A′B′C′即为所求,A′的坐标为:(0,1);
(2)如图所示:△A1B1C1即为所求;
(3)如图所示:△A2B2C2,△A3B3C3,都是符合题意的图形.
 解:(1)如图所示:△A′B′C′即为所求,A′的坐标为:(0,1);
解:(1)如图所示:△A′B′C′即为所求,A′的坐标为:(0,1);(2)如图所示:△A1B1C1即为所求;
(3)如图所示:△A2B2C2,△A3B3C3,都是符合题意的图形.
点评:此题主要考查了旋转变换以及位似变换和平移变换,得出图形变换后对应点位置是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
下列四个函数中,y随x的增大而减小的是( )
| A、y=4x |
| B、y=2x+5 |
| C、y=x-7 |
| D、y=-x+2 |
 如图,某大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和28秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需
如图,某大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶8秒时和28秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 如图,在Rt△ABC中,∠C=90°,已知BC=6,tanA是一元二次方程5x2+2x-3=0的根,请求出AB,AC的长.
如图,在Rt△ABC中,∠C=90°,已知BC=6,tanA是一元二次方程5x2+2x-3=0的根,请求出AB,AC的长.