题目内容
9.如图,抛物线y=ax2+bx+c与x轴交于A(3,0),C(-1,0)两点,与y轴交于点B(0,3),点P为抛物线对称轴上一动点.(1)求抛物线的解析式;
(2)若△PBA的面积与△ABC的面积相等,求点P的坐标;
(3)过点B作BD∥CA,交抛物线于点D,抛物线上是否存在一点E,使∠EBD=∠CBO,若存在,请求出E点坐标;若不存在,请说明理由.

分析 (1)首先设抛物线的解析式为:y=a(x-3)(x+1),直接利用待定系数法求解即可求得答案;
(2)首先求得抛物线的对称轴,求得直线AB的解析式,即可求得直线AB与对称轴的交点坐标,然后设点P的坐标为(1,m),易得$\frac{3}{2}$|m-2|=6,即可求得答案;
(3)首先过点E作BD的垂线,易得△E1BG∽△CBO,△E2BH∽△CBO,继而求得答案.
解答 解:(1)设抛物线的解析式为:y=a(x-3)(x+1),
将B(0,3)代入,3=-3a,
解得:a=-1,
∴抛物线的解析式为:y=-(x-3)(x+1),
即y=-x2+2x+3;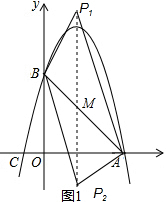
(2)设直线AB的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=3}\\{k=-1}\end{array}\right.$,
∴直线AB的解析式为:y=-x+3,
设直线AB交抛物线对称于点M,
∵抛物线y=ax2+bx+c与x轴交于A(3,0),C(-1,0)两点,
∴对称轴为:x=1,
则M的坐标为(1,2),
∵点P为抛物线对称轴上一动点,
∴设点P的坐标为(1,m),则PM=|m-2|,
∴S△ABP=$\frac{1}{2}$×|m-2|×3=$\frac{3}{2}$|m-2|,S△ABC=$\frac{1}{2}$×4×3=6,
∵△PBA的面积与△ABC的面积相等,
∴$\frac{3}{2}$|m-2|=6,
解得:m=6或m=-2,
∴点P的坐标为(1,6)或(1,-2);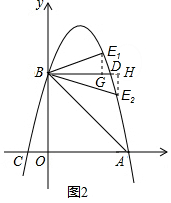 (3)存在.
(3)存在.
如图2,设E的坐标为:(x,-x2+2x+3),
过点E1作E1G⊥BD于点G,则E1G=-x2+2x+3-3=-x2+2x,BG=x,∠BGE=∠BOC=90°,
∵∠EBD=∠CBO,
∴△E1BG∽△CBO,
∴BG:BO=E1G:CO,
∴$\frac{x}{3}=\frac{-{x}^{2}+2x}{1}$,
解得:x1=0(舍去),x2=$\frac{5}{3}$,
∴点E1的坐标为:($\frac{5}{3}$,$\frac{32}{9}$);
过点E2作E2H⊥BD于点H,则E2H=3-(-x2+2x+3)=x2-2x,BH=x,∠BHE=∠BOC=90°,
∵∠EBD=∠CBO,
∴△E2BH∽△CBO,
∴BH:BO=E2H:CO,
∴$\frac{x}{3}=\frac{{x}^{2}-2x}{1}$,
解得:x1=0(舍去),x2=$\frac{7}{3}$,
∴点E2的坐标为:($\frac{7}{3}$,$\frac{20}{9}$);
综上所述:点E的坐标为:($\frac{5}{3}$,$\frac{32}{9}$)或($\frac{7}{3}$,$\frac{20}{9}$).
点评 此题属于二次函数的综合题.考查了待定系数求函数解析式的知识、三角形面积问题以及相似三角形的判定与性质.注意掌握割补法求面积,构造相似三角形是解此题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 2、3、4 | B. | 5、3、8 | C. | 1、3、5 | D. | 1、2、3 |
| A. | $\frac{4}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | 2 |
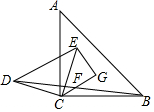 如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.
如图,△ABC和△DEC都是等腰直角三角形,连接BD,F是BD的中点,连接CF并延长至G,使FG=CF,连接EC,CE=10,CF=4,EG=6,则S△ABC=2$\sqrt{130}$.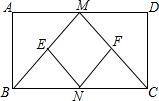 如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点 如图,抛物线y=-x2+mx+n与x轴分别交于点A(4.0),B(-2.0).与y轴交于点C
如图,抛物线y=-x2+mx+n与x轴分别交于点A(4.0),B(-2.0).与y轴交于点C 如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.
如图,在△ABC中,AB=AC,过点B作BD⊥BC,BD=BC,连接AD交BC于点F.E是CD的中点,连接AE交BC于G.