题目内容
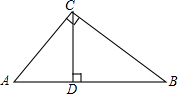
如图，△ABC中∠C=90°，AB的垂直平分线DE交BC于点E，D为垂足，且EC=DE，则∠B的度数为考点：线段垂直平分线的性质
专题：
分析：首先连接AE，由AB的垂直平分线DE交BC于点E，D为垂足，可得AE=BE，又由EC=DE，易证得AE平分∠CAB，继而求得答案．
解答：
解：连接AE，
∵AB的垂直平分线DE交BC于点E，D为垂足，
∴AE=BE，
∴∠EAB=∠B，
∵△ABC中，∠C=90°，且EC=DE，
∴AE平分∠CAB，
∴∠CAE=∠EAB，
∴∠CAB=2∠B，
∵∠CAB+∠B=90°，
∴∠B=30°．
故答案为：30°．
解：连接AE，∵AB的垂直平分线DE交BC于点E，D为垂足，
∴AE=BE，
∴∠EAB=∠B，
∵△ABC中，∠C=90°，且EC=DE，
∴AE平分∠CAB，
∴∠CAE=∠EAB，
∴∠CAB=2∠B，
∵∠CAB+∠B=90°，
∴∠B=30°．
故答案为：30°．
点评：此题考查了线段垂直平分线的性质以及角平分线的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若若|a-b|=|a|-|b|，且a、b均不为0，则有（ ）
| A、a与b同号且|a|≤|b| |
| B、a与b同号且|a|≥|b| |
| C、a与b异号且|a|≤|b| |
| D、a与b异号且|a|≥|b| |
确定一个图形平移后的位置，需要知道平移的（ ）
| A、平移 | B、方向 |
| C、方向和距离 | D、方向或距离 |