题目内容
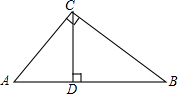如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，若| AD |
| DB |
| 2 |
| 3 |
| AC |
| BC |
考点：相似三角形的判定与性质
专题：
分析：利用直角三角形相似，可得AC2=AD•AB，BC2=BD•AB，再相除，即可得到结论．
解答：解：∵Rt△ABC中，∠ACB=90°，CD⊥AB，
∴△ACD∽△ABC，△BCD∽△BAC，
∴AC2=AD•AB，BC2=BD•AB
∴
=
，
∵AD：BD=2：3，
∴AC：BC=
：
=
：3，
故答案为：
：3．
∴△ACD∽△ABC，△BCD∽△BAC，
∴AC2=AD•AB，BC2=BD•AB
∴
| AC2 |
| BC2 |
| AD |
| BD |
∵AD：BD=2：3，
∴AC：BC=
| 2 |
| 3 |
| 6 |
故答案为：
| 6 |
点评：本题考查三角形的相似，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图，△ABC中∠C=90°，AB的垂直平分线DE交BC于点E，D为垂足，且EC=DE，则∠B的度数为