题目内容
20．已知多项式ax+b与2x2-x+2的乘积展开式中不含x的一次项，且常数项为-4，则ab的值为（ ）| A． | -2 | B． | 2 | C． | -1 | D． | 1 |
分析 利用多项式与多项式相乘的法则求解即可．
解答 解：∵（ax+b）（2x2-x+2）=2ax3+（2b-a）x2+（2a-b）x+2b，
又∵展开式中不含x的一次项，且常数项为-4，
∴$\left\{\begin{array}{l}{2a-b=0}\\{2b=-4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$，
∴ab=（-1）-2=1，
故选D．
点评 本题主要考查了多项式乘多项式，解题的关键正确计算．
练习册系列答案
相关题目
10．
如图，BC是⊙O的直径，点B、C、E、D都在⊙O上，则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（ ）
如图，BC是⊙O的直径，点B、C、E、D都在⊙O上，则$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（ ）| A． | sinA | B． | sin2A | C． | cosA | D． | cos2A |
四边形ABDC在如图所示的平面直角坐标系中，将四边形ABDC向右平移4个单位长度后得四边形A1B1D1C1，再将四边形ABDC绕点O旋转180°后得到四边形A2B2D2C2．
15．
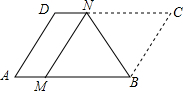如图，将平行四边形纸片ABCD折叠，使顶点C恰好落在AB边上的点M处，折痕为BN，则关于结论：①MN∥AD；②MNCB是菱形．说法正确的是（ ）
如图，将平行四边形纸片ABCD折叠，使顶点C恰好落在AB边上的点M处，折痕为BN，则关于结论：①MN∥AD；②MNCB是菱形．说法正确的是（ ）| A． | ①②都错 | B． | ①对②错 | C． | ①错②对 | D． | ①②都对 |
如图，点B、D、C、F在一条直线上，BC=FD，AB=EF，且AB∥EF．求证：AC∥ED．
如图，一把2.5米长的梯子斜靠在一面竖直的墙壁上，靠墙的一端A与地面的高度AC=1.5米，如果将梯子着地的一端B向墙壁移动0.5米到B′处，那么梯子靠墙的一端A会沿墙壁上升多少米？