题目内容
17.已知x1,x2是方程2x2+3x-4=0的两个根,求$\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$的值.分析 根据根与系数的关系得到x1+x2=-$\frac{3}{2}$,x1x2=-2,再利用通分和完全平方公式变形得到$\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{{x}_{1}}^{2}{{x}_{2}}^{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{({x}_{1}{x}_{2})^{2}}$,然后利用整体代入的方法计算.
解答 解:根据题意得x1+x2=-$\frac{3}{2}$,x1x2=-2,
$\frac{1}{{{x}_{1}}^{2}}$+$\frac{1}{{{x}_{2}}^{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{{x}_{1}}^{2}{{x}_{2}}^{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{({x}_{1}{x}_{2})^{2}}$=$\frac{(-\frac{3}{2})^{2}-2×(-2)}{(-2)^{2}}$=$\frac{25}{16}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
12.如果∠A是锐角,且sinA=cosA,那么∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
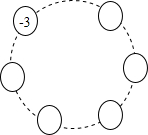 如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少?
如图,请在小圆圈内填满数,使每个小圆圈里的数都是它两旁小圆圈里数的和,并求出所有小圆圈里数的和,如果把原来填的-3改成a,按上面的要求填满后,所有小圆圈里数的和又是多少? 如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少?
如图是抛物线形拱桥,当水面在l时.拱顶离水面2m.水面宽8m.水面下降0.25m.水面宽度增加多少? 如图,在△ABC中.△ACB=90°,点0为三条角平分线的交点,0D⊥BC于D,0E⊥AC于E,0F⊥AB于F,且AB=10cm,CB=6cm,CA=8cm,求0D的长.
如图,在△ABC中.△ACB=90°,点0为三条角平分线的交点,0D⊥BC于D,0E⊥AC于E,0F⊥AB于F,且AB=10cm,CB=6cm,CA=8cm,求0D的长.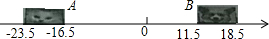 七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
七年级小贝在-张纸上画了-条数轴,妹妹不知它有什么用,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题: 如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形.
如图,△ABC绕点B旋转后,顶点C的对应点D.请确定△ABC旋转后的三角形.