题目内容
9.已知$\frac{x}{{x}^{2}+x+1}$=$\frac{1}{10}$,求$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值.分析 根据$\frac{x}{{x}^{2}+x+1}$=$\frac{1}{10}$,可以求得$x+\frac{1}{x}$的值,从而可以得到${x}^{2}+\frac{1}{{x}^{2}}$的值,然后将$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$变形,即可解答本题.
解答 解:∵$\frac{x}{{x}^{2}+x+1}$=$\frac{1}{10}$,
∴$\frac{1}{x+1+\frac{1}{x}}=\frac{1}{10}$,
∴x+$\frac{1}{x}=9$,
∴$(x+\frac{1}{x})^{2}$=81,
解得,${x}^{2}+\frac{1}{{x}^{2}}=79$,
∴$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$=$\frac{1}{79+1}=\frac{1}{80}$.
点评 本题考查分式的值,解题的关键是明确题意,找出已知式子与所求式子之间的关系.

练习册系列答案
相关题目
18.2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为( )
| A. | 0.456×10-5 | B. | 4.56×10-6 | C. | 4.56×10-7 | D. | 45.6×10-7 |
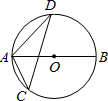 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°. 8个一样大小的长方形恰好拼成一个大的长方形(如图所示),若大长方形的宽为8cm,则每一个小长方形的面积为12cm2.
8个一样大小的长方形恰好拼成一个大的长方形(如图所示),若大长方形的宽为8cm,则每一个小长方形的面积为12cm2.