题目内容
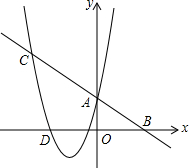 已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.
已知直线y=kx+b分别与y轴、x轴相交于A、B两点,与二次函数y=x2-mx+3的图象交于A、C两点.(1)当点C坐标为(-
| 11 |
| 2 |
| 57 |
| 8 |
(2)在(1)中,如图,将△ABO沿y轴翻折180°,若点B的对应点D恰好落在二次函数y=x2-mx+3的图象上,求点D到直线AB的距离;
(3)当-1≤x≤1时,二次函数y=x2-mx+3有最小值-3,求实数m的值.
考点:二次函数综合题
专题:压轴题
分析:(1)令x=0求出y的值得到点A的坐标,然后设直线AB的解析式为y=kx+b(k≠0),利用待定系数法求一次函数解析式;
(2)令y=0求出点B的坐标,然后根据关于y轴对称的点的横坐标互为相反数求出点D的坐标,然后根据∠ABO的正弦值列式计算即可得解;
(3)表示出抛物线的对称轴,然后根据对称轴的位置,分别根据二次函数的增减性和最值问题列式计算即可得解.
(2)令y=0求出点B的坐标,然后根据关于y轴对称的点的横坐标互为相反数求出点D的坐标,然后根据∠ABO的正弦值列式计算即可得解;
(3)表示出抛物线的对称轴,然后根据对称轴的位置,分别根据二次函数的增减性和最值问题列式计算即可得解.
解答:解:(1)令x=0则y=3,
∴点A(0,3),
设直线AB的解析式为y=kx+b(k≠0),
则
,
解得
,
∴直线AB的解析式为y=-
x+3;
(2)令y=0,则-
x+3=0,
解得x=4,
∴点B(4,0),
点B关于y轴的对称点D的坐标为(-4,0),
∴BD=4-(-4)=4+4=8,
由勾股定理得,AB=
=
=5,
设点D到直线AB的距离为h,
则sin∠ABO=
=
,
即
=
,
解得h=4.8,
即点D到直线AB的距离是4.8;
(3)对称轴为直线x=
,
当
≤-1,即m≤-2时,x=-1时二次函数的最小值为-3,
(-1)2-m•(-1)+3=-3,
解得m=-7;
当-1<
<1,即-2<m<2时,x=
时二次函数有最小值为-3,
=-3,
解得m=±2
,都不满足-2<m<2,舍去;
当
≥1即m≥2时,x=1时二次函数的最小值为-3,
12-m•1+3=-3,
解得m=7,
综上所述,实数m的值为7或-7.
∴点A(0,3),
设直线AB的解析式为y=kx+b(k≠0),
则
|
解得
|
∴直线AB的解析式为y=-
| 3 |
| 4 |
(2)令y=0,则-
| 3 |
| 4 |
解得x=4,
∴点B(4,0),
点B关于y轴的对称点D的坐标为(-4,0),
∴BD=4-(-4)=4+4=8,
由勾股定理得,AB=
| OA2+OB2 |
| 32+42 |
设点D到直线AB的距离为h,
则sin∠ABO=
| h |
| BD |
| OA |
| AB |
即
| h |
| 8 |
| 3 |
| 5 |
解得h=4.8,
即点D到直线AB的距离是4.8;
(3)对称轴为直线x=
| m |
| 2 |
当
| m |
| 2 |
(-1)2-m•(-1)+3=-3,
解得m=-7;
当-1<
| m |
| 2 |
| m |
| 2 |
| 4×1×3-m2 |
| 4×1 |
解得m=±2
| 6 |
当
| m |
| 2 |
12-m•1+3=-3,
解得m=7,
综上所述,实数m的值为7或-7.
点评:本题是二次函数综合题型,主要利用了待定系数法求一次函数解析式,翻折的性质,勾股定理,锐角三角函数的应用,二次函数的最值问题,难点在于(3)根据对称轴的位置情况分情况讨论.

练习册系列答案
相关题目
由下列线段a、b、c组成的三角形为直角三角形的是( )
| A、a=15,b=17,c=8 |
| B、a=4,b=5,c=6 |
| C、a=12,b=60,c=61 |
| D、a=12,b=35,c=36 |
 如图,点M在△ABC的边上,过点M画一条平分三角形面积的直线.
如图,点M在△ABC的边上,过点M画一条平分三角形面积的直线.