题目内容
6.当k为何值时,关于x的方程kx2+kx+2-k=0有两个相等的实数根?此时方程的根是多少呢?分析 根据方程有两个相等的实数根,可得k≠0且△=b2-4ac=0,解方程可得k的值,再把k的值代入方程kx2+kx+2-k=0,解一元二次方程即可.
解答 解:∵关于x的方程程kx2+kx+2-k=0有两个相等的实数根,
∴k≠0且△=b2-4ac=k2-4×(2-k)×k=5k2-8k=0,
解得:k=$\frac{8}{5}$,
∴方程变为:$\frac{8}{5}$x2+$\frac{8}{5}$x+$\frac{2}{5}$=0,
解得x1=x2=-$\frac{1}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
15.下列美丽的图案中,既是轴对称图形又是中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
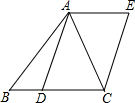 如图,AD是△ABC的中线,四边形ADCE是平行四边形,设BC=a,AC=4,AB=$\sqrt{19}$,要使?ADCE是菱形,a的值是$\sqrt{35}$.
如图,AD是△ABC的中线,四边形ADCE是平行四边形,设BC=a,AC=4,AB=$\sqrt{19}$,要使?ADCE是菱形,a的值是$\sqrt{35}$.