题目内容
6.已知等腰三角形的周长为16,设底边长为x,腰长为y.(1)求出y关于x的函数表达式,并直接写出自变量x的取值范围.
(2)当x=6时,求出y的函数值.
分析 (1)根据三角形的周长公式,可得函数解析式,根据三角形三边的关系,可得自变量的取值范围;
(2)根据自变量与函数值的一一对应关系,可得相应的函数值.
解答 解:(1)由三角形的周长公式,得
y=-$\frac{1}{2}$x+8,
由三角形两边之和大于第三边,得-$\frac{1}{2}$x+8+(-$\frac{1}{2}$x)+8>x
解得0<x<8
写出自变量x的取值范围0<x<8;
(2)当x=6时,y=-$\frac{1}{2}$×6+8=5.
点评 本题考查了函数关系式,利用了三角形的周长公式得出函数关系式,利用三角形三边的关系得出自变量的取值范围.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
1.直线y=3x+m的图象一定经过( )
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第一、三象限 | D. | 第二、三象限 |
16.为迎接“六一”儿童节,某儿童品牌玩具专卖店购进了A、B两类玩具,其中A类玩具的进价比B类玩具的进价每个多3元,经调查:用900元购进A类玩具的数量与用750元购进B类玩具的数量相同.设A类玩具的进价为m元/个,根据题意可列分式方程为( )
| A. | $\frac{900}{m}=\frac{750}{m+3}$ | B. | $\frac{900}{m+3}=\frac{750}{m}$ | C. | $\frac{900}{m}=\frac{750}{m-3}$ | D. | $\frac{900}{m-3}=\frac{750}{m}$ |
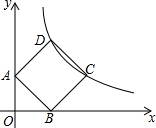 如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.
如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.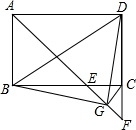 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论: 已知:如图,点E、F分别是?ABCD中AB、DC边上的点,且AE=CF,连接DE、EF.求证:四边形DEBF是平行四边形.
已知:如图,点E、F分别是?ABCD中AB、DC边上的点,且AE=CF,连接DE、EF.求证:四边形DEBF是平行四边形.