题目内容
6．
如图，现有a×a，b×b的正方形纸片和a×b的长方形纸片若干张．（1）若用三种纸片拼一个长为（a+2b）、宽为（a+b）的长方形，那么需要b×b的正方形纸片的张数是2．
（2）利用这些纸片，能否拼成一个面积（2a2+4ab）的长方形？若能，请画出示意图，并用式子表示它的长和宽，若不能，请说明理由；
（3）若用a×a纸片1张，b×b纸片5张，能否拼成一个长方形（或正方形）？
分析 （1）根据多项式乘以多项式可得长方形的面积（a+2b）（a+b）=a2+3ab+2b2，即可解答；
（2）能，理由：因为2a2+4ab=2a（a+2b），所以用2张a×a纸片和4张a×b纸片就可以拼一个长为a+2b，宽为2a的长方形．
（3）不能，因为a2+5b2不能写成两个整系数的积的式子，所以不能拼成一个长方形．
解答 解：（1）根据题意得：（a+2b）（a+b）=a2+3ab+2b2，
则需要b×b的正方形纸片的张数是2，
故答案为：2；
（2）能，如图，
理由：因为2a2+4ab=2a（a+2b），所以用2张a×a纸片和4张a×b纸片就可以拼一个长为a+2b，宽为2a的长方形．
（3）不能，因为a2+5b2不能写成两个整系数的积的式子，所以不能拼成一个长方形．
点评 本题考查了多项式乘以多项式，解决本题的关键是掌握多项式乘以多项式的法则．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
17．母亲节快到了，某校团委随机抽取本校部分同学，进行母亲生日日期了解情况调查，分“知道、不知道、记不清”三种情况．下面图①、图②是根据采集到的数据，绘制的扇形和条形统计图．请根据图中提供的信息，若全校共有990名学生，估计这所学校所有知道母亲的生日的学生人数为（ ）
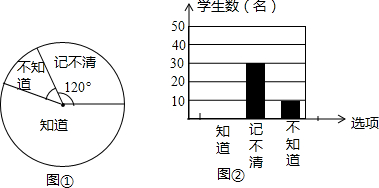
| A． | 440人 | B． | 495人 | C． | 550人 | D． | 6人 |
如图，△ABC中，AB=BC=5，AC=6，过点A作AD∥BC，点P、Q分别是射线AD、线段BA上的动点（不与A、B重合），且AP=BQ，过点P作PE∥AC交线段AQ于点O，连接PQ，设△POQ面积为y，AP=x．
1．不等式3|a|-6≤0的整数解为（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
11．按120分制72分及格未算，满分是150分的及格分是（ ）
| A． | 60分 | B． | 72分 | C． | 90分 | D． | 105分 |
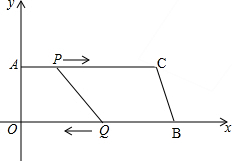如图，在四边形AOBC中，AC∥OB，顶点O是原点，顶点A的坐标为（0，8），AC=24cm，OB=26cm，点P从点A出发，以1cm/s的速度向点C运动，点Q从点B同时出发，以3m/s的速度向点O运动．规定其中一个动点到达端点时，另一个动点也随之停止运动；从运动开始，设P（Q）点运动的时间为ts．