题目内容
16.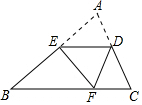 如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )
如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )| A. | 5$\sqrt{3}$cm | B. | 6$\sqrt{3}$cm | C. | 5cm | D. | 4$\sqrt{3}$cm |
分析 根据翻折变换以及E为AB的中点,得出ED∥BC,DE为△ABC的中位线,最后根据△DEF的周长为△ABC周长的一半,即可得出△DEF的周长.
解答 解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AE=EF,∠AED=∠FED,
∵E是AB边的中点,
∴AE=EB,
∴BE=EF=$\frac{1}{2}$AB,
∴∠B=∠BFE=$\frac{1}{2}$∠AEF=∠AED,
∴ED∥BC,
∵E为AB的中点,
∴DE=$\frac{1}{2}$BC,D为AC的中点,
∴DF=AD=$\frac{1}{2}$AC,
∴△DEF的周长为△ABC周长的一半,
即△DEF的周长=$\frac{1}{2}$×12$\sqrt{3}$=6$\sqrt{3}$,
故选:B.
点评 本题考查了翻折变换以及三角形中位线的运用,解题时注意掌握翻折变换的性质:翻折前后对应边相等、对应角相等.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
9.下列各式能用平方差公式计算的是( )
| A. | (-2x-1)(1-2x) | B. | (x-3)(3-x) | C. | (x-3)(2x+3) | D. | (-x-3)(x+3) |
7.下列说法中,错误的是( )
| A. | -9没有平方根 | B. | 4的算术平方根是2 | ||
| C. | 8的平方根是±2$\sqrt{2}$ | D. | 8的立方根是±2 |
4.在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应边中点的连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有( )
| A. | ①②③④ | B. | ①②③④⑤ | C. | ①②③⑤ | D. | ①③④⑤ |
11.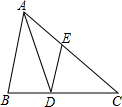 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
 如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )
如图,已知AD为△ABC的角平分线,DE∥AB交AC于E,如果$\frac{CE}{AC}=\frac{3}{5}$,那么$\frac{AE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
1. 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{CG}{DG}$=$\frac{CF}{BF}$ | B. | $\frac{EG}{FG}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{BD}$ | D. | $\frac{EF}{AB}$=$\frac{CG}{CD}$ |
8.下列运算中,正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a6 | C. | a6÷a2=a4 | D. | 2(a+b)=2a+b |
5.下列根式中,最简二次根式是( )
| A. | $\sqrt{25}$ | B. | -$\sqrt{12}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{10}$ |
3.若△ABC与△DEF全等,且∠A=60°,∠B=70°,则∠D的度数不可能是( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |