题目内容
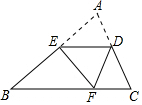
1. 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )| A. | $\frac{CG}{DG}$=$\frac{CF}{BF}$ | B. | $\frac{EG}{FG}$=$\frac{AD}{BD}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{BD}$ | D. | $\frac{EF}{AB}$=$\frac{CG}{CD}$ |
分析 由DE∥BC,EF∥AB,根据平行线分线段成比例定理.利用排除法即可求得答案.
解答 解:A、∵DE∥BC,EF∥AB,∴$\frac{CG}{DG}=\frac{CF}{DE}$,错误;
B、∵DE∥BC,EF∥AB,∴$\frac{EG}{EC}=\frac{AD}{BD}$,错误;
C、∵DE∥BC,EF∥AB,∴$\frac{DE}{BC}=\frac{AD}{AB}$,错误;
D、∵DE∥BC,EF∥AB,∴$\frac{EF}{AB}=\frac{CG}{CD}$,正确;
故选D
点评 此题考查了平行线分线段成比例定理.此题难度不大,解题的关键注意找到对应线段,注意数形结合思想的应用.

练习册系列答案
相关题目
14.若一个数的算术平方根与它的立方根相同,则这个数是( )
| A. | 0 | B. | ±1 | C. | 0和±1 | D. | 0和1 |
12.下列各组长度的线段能构成三角形的是( )
| A. | 1.5 cm,3.9 cm,2.3 cm | B. | 3.5 cm,7.1 cm,3.6 cm | ||
| C. | 6 cm,1 cm,6 cm | D. | 4 cm,10 cm,4 cm |
9. 如图,在△ABC纸片中,∠BAC=50°,将△ABC纸片绕点A按逆时针方向旋转50°,得到△ADE,此时AD边经过点C,连接BD,若∠DBC的度数为40°,则∠ACB的度数为( )
如图,在△ABC纸片中,∠BAC=50°,将△ABC纸片绕点A按逆时针方向旋转50°,得到△ADE,此时AD边经过点C,连接BD,若∠DBC的度数为40°,则∠ACB的度数为( )
 如图,在△ABC纸片中,∠BAC=50°,将△ABC纸片绕点A按逆时针方向旋转50°,得到△ADE,此时AD边经过点C,连接BD,若∠DBC的度数为40°,则∠ACB的度数为( )
如图,在△ABC纸片中,∠BAC=50°,将△ABC纸片绕点A按逆时针方向旋转50°,得到△ADE,此时AD边经过点C,连接BD,若∠DBC的度数为40°,则∠ACB的度数为( )| A. | 115° | B. | 105° | C. | 80° | D. | 95° |
16. 如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )
如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )
 如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )
如图,E是AB边上的中点,将△ABC沿过E的直线折叠,使点A落在BC上F处,折痕交边AC于点D,若△ABC的周长为12$\sqrt{3}$,则△DEF的周长是( )| A. | 5$\sqrt{3}$cm | B. | 6$\sqrt{3}$cm | C. | 5cm | D. | 4$\sqrt{3}$cm |
6.将函数y=-2x的图象向下平移3个单位后与y轴的交点坐标为( )
| A. | (-3,0) | B. | ($\frac{3}{2}$,0) | C. | (0,3) | D. | (0,-3) |
13. 如图,若△ABC经过平移后得到△A1B1C1,已知点C的对应点C1的坐标为(4,0),则点A的对应点A1的坐标为( )
如图,若△ABC经过平移后得到△A1B1C1,已知点C的对应点C1的坐标为(4,0),则点A的对应点A1的坐标为( )
 如图,若△ABC经过平移后得到△A1B1C1,已知点C的对应点C1的坐标为(4,0),则点A的对应点A1的坐标为( )
如图,若△ABC经过平移后得到△A1B1C1,已知点C的对应点C1的坐标为(4,0),则点A的对应点A1的坐标为( )| A. | (0,2) | B. | (2,3) | C. | (2,2) | D. | (1,2) |
10.下列语句:(1)经过两点有且只有一条直线;(2)过两点的连线中,直线最短;(3)在同一平面内,三条直线的交点可能有1个或3个;(4)连接两点的线段叫做两点间的距离;其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.下列计算正确的是( )
| A. | 23=6 | B. | -42=16 | C. | -8-8=0 | D. | -5+2=-3 |