题目内容
15. 如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.
如图,AB是斜靠在墙角的长梯,梯角B距墙0.8m,长梯上一点D距墙0.7m,BD长0.55m,则梯子的长度是4.4m.
分析 由DE∥BC可得△ADE∽△ABC,进而利用相似三角形的对应边成比例可得梯子AB的长.
解答 解:∵DE⊥AC,AC⊥CB,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,
∴$\frac{AB-0.55}{AB}=\frac{0.7}{0.8}$
解得AB=4.4.
答:梯子长4.4m.
故答案为:4.4.
点评 本题考查了相似三角形的应用;用到的知识点为:两角对应成比例且夹角相等的两三角形相似;相似三角形的对应边成比例.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
6.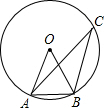 点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )
点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )
 点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )
点B在⊙O上,点C是⊙O上异于A、B的一点,若∠AOB=50°,则∠ACB的度数是( )| A. | 25° | B. | 65° | C. | 30° | D. | 25°、155° |
7.等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 55°或130° |
5. 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )| A. | (2,5) | B. | (2.5,5) | C. | (3,5) | D. | (3,6) |
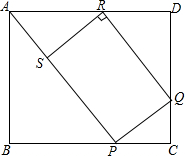 如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.
如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S. 如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是54a2.
如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是54a2.