题目内容
20.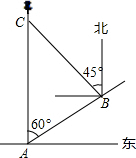 如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.
如图,一船在灯塔C的正南方向A处,上午10时,该船从A处沿北偏东60°方向航行,速度为20海里/时,中午13时到达B处,测得灯塔C在其北偏西45°方向上,试求此时船和灯塔的距离BC.
分析 过点B作BD⊥AC于D,解Rt△ABD,得出AD=$\frac{1}{2}$AB=30,BD=$\sqrt{3}$AD=30$\sqrt{3}$,再由△BCD是等腰直角三角形,得到BC=$\sqrt{2}$BD=30$\sqrt{6}$.
解答 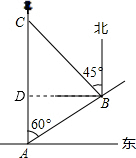 解:过点B作BD⊥AC于D.
解:过点B作BD⊥AC于D.
在Rt△ABD中,∵∠ADB=90°,∠DAB=60°,
∴∠ABD=30°,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×20×3=30,BD=$\sqrt{3}$AD=30$\sqrt{3}$,
在Rt△BCD中,∵∠CDB=90°,∠CBD=45°,
∴BC=$\sqrt{2}$BD=$\sqrt{2}$×30$\sqrt{3}$=30$\sqrt{6}$.
答:此时船和灯塔的距离BC为30$\sqrt{6}$海里.
点评 本题考查解直角三角形的应用-方向角问题,准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
5. 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
 如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )| A. | (2,5) | B. | (2.5,5) | C. | (3,5) | D. | (3,6) |
12. 如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
 如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )
如图所示,OC平分∠AOB,OD平分∠AOC,且∠COD=25°,则∠AOB等于( )| A. | 50° | B. | 75° | C. | 100° | D. | 20° |
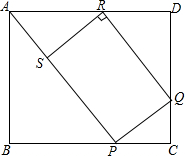 如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.
如图所示,矩形ABCD中,AB=1,BC=x,P,Q分别是BC,CD,DA上的点,且∠BAP=45°,CP=CQ,RQ∥AP.RS⊥AP于点S.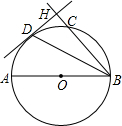 如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.
如图,已知AB为⊙O的直径,弦BD平分∠ABH,过点D作DH⊥BH于点H,BH交⊙O于点C.