题目内容
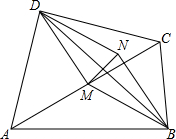 已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.
已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.(1)求证:四边形BMDN是菱形;
(2)若∠BAC=30°,∠ACD=45°,求菱形BNDM相邻两角的度数.
考点:菱形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得BM=DM=
AC,设BD与MN相交于点O,根据等腰三角形三线合一可得BO=DO,再根据两直线平行,内错角相等可得∠MDO=∠NBO,然后利用“角边角”证明△MDO和△NBD全等,根据全等三角形对应边相等可得OM=ON,然后根据对角线互相垂直平分的四边形是菱形证明即可;
(2)根据等腰三角形的性质求出∠BMC,再根据等腰直角三角形的性质求出∠CMD=90°,然后求出∠BMD,再根据菱形的邻角互补列式计算即可求出∠MBN.
| 1 |
| 2 |
(2)根据等腰三角形的性质求出∠BMC,再根据等腰直角三角形的性质求出∠CMD=90°,然后求出∠BMD,再根据菱形的邻角互补列式计算即可求出∠MBN.
解答: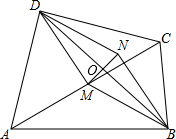 (1)证明:∵∠ABC=∠ADC=90°,M是AC中点,
(1)证明:∵∠ABC=∠ADC=90°,M是AC中点,
∴BM=DM=
AC,
设BD与MN相交于点O,
∵MN⊥BD,
∴BO=DO,
∵MD∥BN,
∴∠MDO=∠NBO,
在△MDO和△NBD中,
,
∴△MDO≌△NBD(ASA),
∴OM=ON,
∴BD、MN互相垂直平分,
∴四边形BMDN是菱形;
(2)解:∵∠BAC=30°,∠ACD=45°,
∴∠BMC=30°×2=60°,
∠CMD=90°,
∴∠BMD=60°+90°=150°,
∵DM∥BN,
∴∠MBN=180°-150°=30°,
∴菱形BNDM相邻两角的度数是150°,30°.
 (1)证明:∵∠ABC=∠ADC=90°,M是AC中点,
(1)证明:∵∠ABC=∠ADC=90°,M是AC中点,∴BM=DM=
| 1 |
| 2 |
设BD与MN相交于点O,
∵MN⊥BD,
∴BO=DO,
∵MD∥BN,
∴∠MDO=∠NBO,
在△MDO和△NBD中,
|
∴△MDO≌△NBD(ASA),
∴OM=ON,
∴BD、MN互相垂直平分,
∴四边形BMDN是菱形;
(2)解:∵∠BAC=30°,∠ACD=45°,
∴∠BMC=30°×2=60°,
∠CMD=90°,
∴∠BMD=60°+90°=150°,
∵DM∥BN,
∴∠MBN=180°-150°=30°,
∴菱形BNDM相邻两角的度数是150°,30°.
点评:本题考查了菱形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,等腰直角三角形的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知3xa-2是关于x的三次单项式,那么a的值为( )
| A、4 | B、5 | C、6 | D、7 |
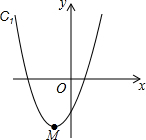 如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为
如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为下列四边形一定有内切圆的是( )
| A、平行四边形 | B、菱形 |
| C、等腰梯形 | D、矩形 |
在Rt△ABC中,∠C=90°,sinA=
.则cosB的值为( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
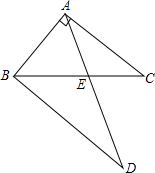 如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )
如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )| A、15°或30° |
| B、30°或45° |
| C、15°或45° |
| D、30°或60° |