题目内容
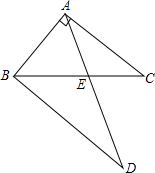 如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )
如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )| A、15°或30° |
| B、30°或45° |
| C、15°或45° |
| D、30°或60° |
考点:旋转的性质
专题:计算题
分析:由∠BAC=90°,AB=AC可判断△ABC为等腰直角三角形,则∠ABC=∠ACB=45°,再由BD∥AC得∠ABD=∠BAC=90°,则利用互余可计算出∠BAD=60°,由于把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,而等腰三角形的腰不能确定,所以分类讨论:当AE=AF时,如图1,根据旋转的性质得∠BAB′=α,∠B′AD=60°,可判断△AEF为等边三角形,得到∠1=∠2=60°,则可根据三角形外角性质可计算出∠BAB′=∠1-∠ABC=15°,即α=15°;当AFA=FC时,如图2,∠BAB′=α,根据等腰三角形的性质得∠ACB=∠FAC=45°,所以∠BAB′=45°,即α=45°,由此得到α的值为15°或45°.
解答:解: ∵∠BAC=90°,AB=AC,
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵BD∥AC,
∴∠ABD=∠BAC=90°,
∵∠D=30°,
∴∠BAD=60°,
把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,
当AE=AF时,如图1,则∠BAB′=α,∠B′AD=60°,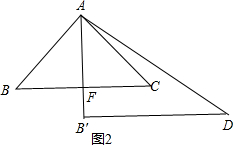
∴△AEF为等边三角形,
∴∠1=∠2=60°,
而∠1=∠B+∠BAB′,
∴∠BAB′=60°-45°=15°,
即α=15°;
当AFA=FC时,如图2,则∠BAB′=α,
∵∠ACB=45°,
∴∠FAC=45°,
∴∠BAB′=90°-45°=45°,
即α=45°;
综上所述,α的值为15°或45°.
故选C.
 ∵∠BAC=90°,AB=AC,
∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵BD∥AC,
∴∠ABD=∠BAC=90°,
∵∠D=30°,
∴∠BAD=60°,
把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,
当AE=AF时,如图1,则∠BAB′=α,∠B′AD=60°,

∴△AEF为等边三角形,
∴∠1=∠2=60°,
而∠1=∠B+∠BAB′,
∴∠BAB′=60°-45°=15°,
即α=15°;
当AFA=FC时,如图2,则∠BAB′=α,
∵∠ACB=45°,
∴∠FAC=45°,
∴∠BAB′=90°-45°=45°,
即α=45°;
综上所述,α的值为15°或45°.
故选C.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
相关题目
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、5
| ||||||||
D、2
|
下列式子不正确的是( )
| A、|-4|=4 | ||||
B、|
| ||||
| C、|0|=0 | ||||
| D、|-1.5|=-1.5 |
 如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.
如图,延长线段AB到C,使BD=3AB,点D是线段BC的中点,CD=6,求线段AC的长.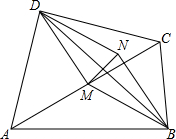 已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.
已知如图,四边形ABCD中,∠ABC=∠ADC=90°,M是AC中点,MN⊥BD且与MD的平行线BN相交于N.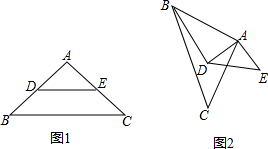 已知在△ABC中,AB=AC,DE分别是AB,AC的中点,将ABC绕点A顺时针旋转a角(0°<a<180°),得到AB′C′,(如图2),探究DB′与EC′的数量关系,并加以证明.
已知在△ABC中,AB=AC,DE分别是AB,AC的中点,将ABC绕点A顺时针旋转a角(0°<a<180°),得到AB′C′,(如图2),探究DB′与EC′的数量关系,并加以证明. 根据如图所示数值转换器,当输出的值为y=6时,输入值x为
根据如图所示数值转换器,当输出的值为y=6时,输入值x为