题目内容
17.下列各对数中,互为相反数的是( )| A. | -(-3)和3 | B. | +(-5)和-[-(-5)] | C. | $\frac{1}{3}$和-3 | D. | -(-7)和-|-7| |
分析 根据绝对值的含义和求法,以及相反数的含义以及求法,逐一判断出互为相反数的是哪组数即可.
解答 解:∵-(-3)=3,
∴-(-3)和3相等,不互为相反数,
∴选项A不正确;
∵+(-5)=-5,-[-(-5)]=-5,
∴+(-5)=-5和-[-(-5)]相等,不互为相反数,
∴选项B不正确;
∵$\frac{1}{3}$和-$\frac{1}{3}$互为相反数,$\frac{1}{3}$和-3不互为相反数,
∴选项C不正确;
∵-(-7)=7,-|-7|=-7,
∴-(-7)和-|-7|互为相反数,
∴选项D正确.
故选:D.
点评 此题主要考查了绝对值的含义和求法,以及相反数的含义以及求法,要熟练掌握,解答此题的关键是要明确:相反数是成对出现的,不能单独存在;求一个数的相反数的方法就是在这个数的前边添加“-”.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8. 如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
 如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是( )| A. | ∠B=∠C | B. | ∠D=∠E | C. | ∠DAE=∠BAC | D. | ∠CAD=∠DAC |
12.下列语句正确的有( )
①直径是弦;
②半圆是弧;
③长度相等的弧是等弧;
④经过圆内一定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
①直径是弦;
②半圆是弧;
③长度相等的弧是等弧;
④经过圆内一定点可以作无数条弦;
⑤经过圆内一定点可以作无数条直径.
| A. | 3 个 | B. | 2个 | C. | 1 个 | D. | 4个 |
2.将抛物线y=(x-4)2+2向右平移1个单位,再向下平移3个单位,则平移后抛物线的表达式为( )
| A. | y=(x-3)2+5 | B. | y=(x-3)2-1 | C. | y=(x-5)2+5 | D. | y=(x-5)2-1 |
9. 如图,在一幅长60cm,宽40cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是3100cm2,设金色纸边的宽为x cm,则满足的方程是( )
如图,在一幅长60cm,宽40cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是3100cm2,设金色纸边的宽为x cm,则满足的方程是( )
 如图,在一幅长60cm,宽40cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是3100cm2,设金色纸边的宽为x cm,则满足的方程是( )
如图,在一幅长60cm,宽40cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是3100cm2,设金色纸边的宽为x cm,则满足的方程是( )| A. | (60+x)(40+x)=3100 | B. | (60+2x)(40+2x)=3100 | C. | (60+2x)(40+x)=3100 | D. | (60+x)(40+2x)=3100 |
6.-$\frac{1}{3}$绝对值的相反数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为3.2米.
如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为3.2米.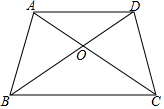 已知梯形ABCD如图,AD∥BC,△AOD的面积是25,△DOC的面积是35,则梯形ABCD的面积是144.
已知梯形ABCD如图,AD∥BC,△AOD的面积是25,△DOC的面积是35,则梯形ABCD的面积是144.