题目内容
7．解方程组（1）$\left\{\begin{array}{l}3x+2y=14\\ 3x-4y=2\end{array}\right.$
（2）$\left\{\begin{array}{l}2x+3y=13\\ 3x+1=y+4\end{array}\right.$．
分析 （1）方程组利用加减消元法求出解即可；
（2）方程组整理后，利用加减消元法求出解即可．
解答 解：（1）$\left\{\begin{array}{l}{3x+2y=14①}\\{3x-4y=2②}\end{array}\right.$，
①-②得：6y=12，即y=2，
把y=2代入①得：x=$\frac{10}{3}$，
则方程组的解为$\left\{\begin{array}{l}{x=\frac{10}{3}}\\{y=2}\end{array}\right.$；
（2）方程组整理得：$\left\{\begin{array}{l}{2x+3y=13①}\\{3x-y=3②}\end{array}\right.$，
①+②×3点到：11x=22，即x=2，
把x=2代入②得：y=3，
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
名校课堂系列答案
相关题目
如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD=25°10′，则∠AOB的度数为100°40′．
18．
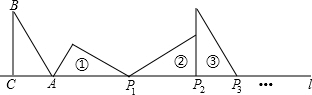如图，在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针转到位置①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=3+$\sqrt{3}$；…，按此顺序继续旋转，得到点P2016，则AP2016=（ ）
如图，在△ABC中，∠ACB=90°，∠B=30°，AC=1，AC在直线l上，将△ABC绕点A顺时针转到位置①，可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=3+$\sqrt{3}$；…，按此顺序继续旋转，得到点P2016，则AP2016=（ ）| A． | 2016+671$\sqrt{3}$ | B． | 2016+672$\sqrt{3}$ | C． | 2017+672$\sqrt{3}$ | D． | 2016+673$\sqrt{3}$ |
2．城市轨道交通的建设为市民的出行提供了很多便利，根据成都市城市轨道交通第三期的建设规定（2016至2020年），至2020年，我市将形成13条线路，总长508000米的轨道交通网．将508000用科学记数法表示为（ ）
| A． | 5.08×106 | B． | 5.08×105 | C． | 0.508×106 | D． | 50.8×104 |
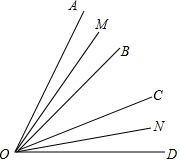如图，OB、OC是∠AOD的两条射线，OM和ON分别是∠AOB和∠COD内部的一条射线，且∠AOD=α，∠MON=β．
16．化简$\frac{2x}{x-2}$+$\frac{x}{2-x}$的结果是（ ）
| A． | x | B． | x-1 | C． | $\frac{3x}{x-2}$ | D． | $\frac{x}{x-2}$ |
