题目内容
1.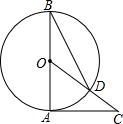 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D.连接BD,若∠C=40°,则∠ODB的度数为25°.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D.连接BD,若∠C=40°,则∠ODB的度数为25°.
分析 先根据切线的性质得∠OAC=90°,再利用互余计算出∠AOC=90°-∠C=50°,由于∠OBD=∠ODB,利用三角形的外角性质得∠ODB=$\frac{1}{2}$∠AOC=25°.
解答 解:∵AC是⊙O的切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠AOC=90°-∠C=90°-40°=50°,
∵OB=OD,
∴∠OBD=∠ODB,
而∠AOC=∠OBD+∠ODB,
∴∠ODB=$\frac{1}{2}$∠AOC=25°,
故答案为:25°
点评 本题考查了切线的性质,三角形外角性质,三角形内角和定理,等腰三角形性质的应用,解此题的关键是求出∠AOC的度数.

练习册系列答案
相关题目
6.若关于x的一元二次方程x2-4x+5-a=0有实数根,则a的取值范围是( )
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
7.已知a=$\frac{{\sqrt{2}}}{2}$,b=$\frac{{\sqrt{3}}}{3}$,c=$\frac{{\sqrt{5}}}{5}$,则下列大小关系正确的是( )
| A. | a>b>c | B. | c>b>a | C. | b>a>c | D. | a>c>b |
9.在平面直角坐标系中,点(4,-5)关于x轴对称点的坐标为( )
| A. | (4,5) | B. | (-4,-5) | C. | (-4,5) | D. | (5,4) |
16.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | 1-$\frac{1}{7}$ | D. | $\sqrt{2}$ |
13.不等式组$\left\{\begin{array}{l}\frac{x-3}{2}+3≥x+1\\ 1-3(x-1)<8-x\end{array}\right.$的整数解是( )
| A. | -2,-1,0 | B. | -1,0,1 | C. | 0,1,2 | D. | 1,2,3 |
11.抛物线y=x2+6x的对称轴是( )
| A. | 直线x=-3 | B. | 直线x=6 | C. | 直线x=3 | D. | 直线x=-6 |