题目内容
6．若关于x的一元二次方程x2-4x+5-a=0有实数根，则a的取值范围是（ ）| A． | a≥1 | B． | a＞1 | C． | a≤1 | D． | a＜1 |
分析 根据关于x的一元二次方程x2-4x+5-a=0有实数根，得出△=16-4（5-a）≥0，从而求出a的取值范围．
解答 解：∵关于x的一元二次方程x2-4x+5-a=0有实数根，
∴△=（-4）2-4（5-a）≥0，
∴a≥1．
故选A．
点评 此题主要考查了一元二次方程根的情况与判别式，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
16．中国人口众多，地大物博，仅领水面积就约为370 000km2，将“370 000”这个数用科学记数法表示为（ ）
| A． | 3.7×106 | B． | 3.7×105 | C． | 37×104 | D． | 3.7×104 |
17．当1≤x≤2时，ax+2＞0，则a的取值范围是（ ）
| A． | a＞-1 | B． | a＞-2 | C． | a＞0 | D． | a＞-1且a≠0 |
14．若关于x的方程x2+2x+a=0不存在实数根，则a的取值范围是（ ）
| A． | a＜1 | B． | a＞1 | C． | a≤1 | D． | a≥1 |
18．某商店举办促销活动，促销的方法是将原价x元的衣服以（$\frac{4}{5}$x-10）元出售，则下列说法中，能正确表达该商店促销方法的是（ ）
| A． | 原价减去10元后再打8折 | B． | 原价打8折后再减去10元 | ||
| C． | 原价减去10元后再打2折 | D． | 原价打2折后再减去10元 |
15．已知x=2-$\sqrt{3}$，则代数式（7+4$\sqrt{3}$）x2+（2+$\sqrt{3}$）x+$\sqrt{3}$的值是（ ）
| A． | 0 | B． | $\sqrt{3}$ | C． | 2+$\sqrt{3}$ | D． | 2-$\sqrt{3}$ |
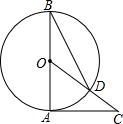如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D．连接BD，若∠C=40°，则∠ODB的度数为25°．