题目内容
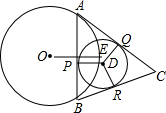 如图,OE是⊙O的半径,弦AB垂直平分OE,点D是
如图,OE是⊙O的半径,弦AB垂直平分OE,点D是 |
| AEB |
(1)求∠ACB的度数;
(2)若⊙O半径为6,⊙D半径为2,求△ABC的周长.
考点:切线的性质
专题:
分析:(1)连接DA、DB、OA、OB,则由条件可知AD、BD分别平分∠BAC和∠ABC,则可得∠ACB=180°-2(∠BAD+∠ABD)=180°-∠AOB,由条件可求得∠AOB=120°,可求得∠ACB;
(2)由⊙O半径为6,可求得AB的长,由⊙D半径为2,可求得CD和CR的长,则可求得△ABC的周长为2AB+2CQ,计算即可.
(2)由⊙O半径为6,可求得AB的长,由⊙D半径为2,可求得CD和CR的长,则可求得△ABC的周长为2AB+2CQ,计算即可.
解答:解:(1)如图1,连接DA、DB、OA、OB、OD,
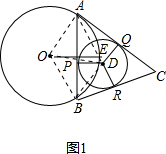
由题可知D为△ABC的内心,
∴AD平分∠BAC,BD平分∠ABC,
∴∠ACB=180°-∠ABC-∠BAC=180°-2(∠DAB+∠DBA),
∵OE是⊙O的半径,弦AB垂直平分OE,
∴∠OAB=∠OBA=30°,
∴∠AOB=120°,
且∠DOB=2∠DAB,∠BOA=2∠DBA,
∴∠ACB=180°-2(∠DAB+∠DBA)=180°-∠AOB=60°;
(2)如图2,连接CD,
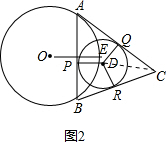
由(1)可知∠AOE=∠BOE=60°,且OA=OB=6,
∴AB=6
,
在Rt△DQC中,DQ=2,∠DCQ=
∠ACB=30°,
∴CQ=2
,
又∵AB、AC、BC都为切线,
∴AP=AQ,BP=BR,CQ=CR,
∴AB+AC+BC=AB+AQ+BR+CQ+CR=2AB+2CQ=12
+4
=16
,
即△ABC的周长为16
.

由题可知D为△ABC的内心,
∴AD平分∠BAC,BD平分∠ABC,
∴∠ACB=180°-∠ABC-∠BAC=180°-2(∠DAB+∠DBA),
∵OE是⊙O的半径,弦AB垂直平分OE,
∴∠OAB=∠OBA=30°,
∴∠AOB=120°,
且∠DOB=2∠DAB,∠BOA=2∠DBA,
∴∠ACB=180°-2(∠DAB+∠DBA)=180°-∠AOB=60°;
(2)如图2,连接CD,

由(1)可知∠AOE=∠BOE=60°,且OA=OB=6,
∴AB=6
| 3 |
在Rt△DQC中,DQ=2,∠DCQ=
| 1 |
| 2 |
∴CQ=2
| 3 |
又∵AB、AC、BC都为切线,
∴AP=AQ,BP=BR,CQ=CR,
∴AB+AC+BC=AB+AQ+BR+CQ+CR=2AB+2CQ=12
| 3 |
| 3 |
| 3 |
即△ABC的周长为16
| 3 |
点评:本题主要考查切线的性质及圆周角定理、切线长定理,由条件得到D为△ABC的内心是解题的关键,注意角平分线和切线长定理的应用.

练习册系列答案
相关题目
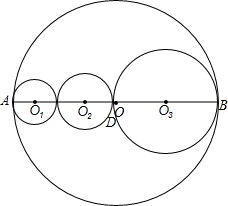 如图,点C、D在线段AB上,⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB.
如图,点C、D在线段AB上,⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB. 如图,E为AD的中点,BE平分∠ABC,且AB+CD=BC,求证:CE平分∠BCD.
如图,E为AD的中点,BE平分∠ABC,且AB+CD=BC,求证:CE平分∠BCD. 已知△ABC中,CA=CB,点O为AB的中点,∠ACB=120°,EF分别在直线AC、BC上,且∠EOF=60°.
已知△ABC中,CA=CB,点O为AB的中点,∠ACB=120°,EF分别在直线AC、BC上,且∠EOF=60°.