题目内容
12.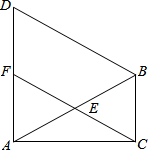 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.
如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.(1)求证:△AEF≌△BEC;
(2)连接BF,试判定BF与AD的位置关系,并说明理由.
分析 (1)求出∠FAE=∠EBC,根据ASA推出两三角形全等即可;
(2)先推出四边形AFBC是矩形,根据矩形的性质得出∠AFB=90°,即可得出答案.
解答 (1)证明:∵△ABD是等边三角形,
∴∠DAB=60°,
∵∠CAB=30°,∠ACB=90°,
∴∠EBC=180°-90°-30°=60°,
∴∠FAE=∠EBC,
∵E为AB的中点,
∴AE=BE,
在△AEF和△BEC中
$\left\{\begin{array}{l}{∠FAE=∠EBC}\\{AE=BE}\\{∠FEA=∠BEC}\end{array}\right.$
∴△AEF≌△BEC(ASA);
(2)解:BF⊥AD,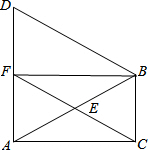
理由是:∵△AEF≌△BEC,
∴EF=EC,
∵AE=BE,
∴四边形AFBC是平行四边形,
∵∠ACB=90°,
∴四边形AFBC是矩形,
∴∠BFA=90°,
∴BF⊥AD.
点评 本题考查了等边三角形的性质,矩形的性质和判定,全等三角形的性质和判定的应用,能推出△AEF≌△BEC是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.将抛物线y=-(x+1)2向左平移1个单位后,得到的抛物线的顶点坐标是( )
| A. | (-2,0) | B. | (0,0) | C. | (-1,-1) | D. | (-2,-1) |
1.代数式2x+3与5互为相反数,则x等于( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
 用8个相同的小正方体搭成一个几何体,从上面看它得到的平面图形如图所示,那么从左面看它得到的平面图形一定不是( )
用8个相同的小正方体搭成一个几何体,从上面看它得到的平面图形如图所示,那么从左面看它得到的平面图形一定不是( )



 如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,若∠A=80°,则∠BDC=50°.
如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,若∠A=80°,则∠BDC=50°.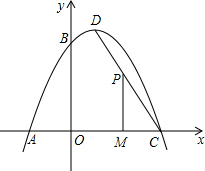 如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.