题目内容
20. 如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,若∠A=80°,则∠BDC=50°.
如图,BD与CD分别平分∠ABC、∠ACB的外角∠EBC、∠FCB,若∠A=80°,则∠BDC=50°.
分析 先根据BD、CD分别是∠CBE、∠BCF的平分线可知∠DBC=$\frac{1}{2}$∠EBC,∠BCD=$\frac{1}{2}$∠BCF,再由∠CBE、∠BCF是△ABC的两个外角得出∠CBE+∠BCF=180°+∠A=260°,故∠DBC+∠BCD=$\frac{1}{2}$(∠EBC+∠BCF)=130°,根据三角形内角和定理求出即可.
解答 证明:BD、CD分别是∠CBE、∠BCF的平分线
∴∠DBC=$\frac{1}{2}$∠EBC,∠BCD=$\frac{1}{2}$∠BCF,
∵∠CBE、∠BCF是△ABC的两个外角
∴∠CBE+∠BCF=360°-(180°-∠A)=180°+∠A=260°,
∴∠DBC+∠BCD=$\frac{1}{2}$(∠EBC+∠BCF)=130°
在△DBC中,∠BDC=180°-(∠DBC+∠BCD)=180°-130°=50°,
故答案为:50°.
点评 本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
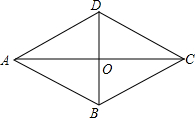 如图,在?ABCD中,AC与BD相交于点O,OA=3,OB=2,AB=$\sqrt{13}$,试判断?ABCD是菱形还是矩形?请说明理由.
如图,在?ABCD中,AC与BD相交于点O,OA=3,OB=2,AB=$\sqrt{13}$,试判断?ABCD是菱形还是矩形?请说明理由. 以下是一位同学所做的有理数运算解题过程的一部分:
以下是一位同学所做的有理数运算解题过程的一部分: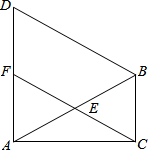 如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.
如图,在△ABC中,∠ACB=90°,∠CAB=30°,以AB为边在△ABC外作等边△ABD,E是AB的中点,连接CE并延长交AD于F.