题目内容
15.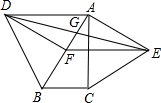 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和等边△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据直角三角形斜边上的中线等于斜边的一半,可得FA=FC,根据等边三角形的性质可得EA=EC,根据线段垂直平分线的判定可得EF是线段AC的垂直平分线;根据条件及等边三角形的性质可得∠DFA=∠EAF=90°,DA⊥AC,从而得到DF∥AE,DA∥EF,可得到四边形ADFE为平行四边形而不是菱形;根据平行四边形的对角线互相平分可得AD=AB=2AF=4AG;易证DB=DA=EF,∠DBF=∠EFA=60°,BF=FA,即可得到△DBF≌△EFA.
解答 解: 连接FC,如图所示:
连接FC,如图所示:
∵∠ACB=90°,F为AB的中点,
∴FA=FB=FC,
∵△ACE是等边三角形,
∴EA=EC,
∵FA=FC,EA=EC,
∴点F、点E都在线段AC的垂直平分线上,
∴EF垂直平分AC,即EF⊥AC;
∵△ABD和△ACE都是等边三角形,F为AB的中点,
∴DF⊥AB即∠DFA=90°,BD=DA=AB=2AF,∠DBA=∠DAB=∠EAC=∠ACE=60°.
∵∠BAC=30°,
∴∠DAC=∠EAF=90°,
∴∠DFA=∠EAF=90°,DA⊥AC,
∴DF∥AE,DA∥EF,
∴四边形ADFE为平行四边形而不是菱形;
∵四边形ADFE为平行四边形,
∴DA=EF,AF=2AG,
∴BD=DA=EF,DA=AB=2AF=4AG;
在△DBF和△EFA中,
$\left\{\begin{array}{l}{BD=FE}\\{∠DBF=∠EFA}\\{BF=FA}\end{array}\right.$,
∴△DBF≌△EFA;
综上所述:①③④正确,
故选C.
点评 本题主要考查了直角三角形斜边上的中线等于斜边的一半、等边三角形的性质、线段垂直平分线的判定、平行四边形判定与性质、全等三角形的判定与性质等知识;本题综合性比较强,有一定难度.

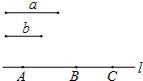 尺规作图:如图,已知线段a,b.
尺规作图:如图,已知线段a,b.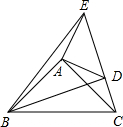 如图,在等腰Rt△ABC和等腰Rt△ADE中,∠BAC=∠DAE=90°,点C、D、E在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④BE2=2(AD2+AB2).其中,结论正确的个数是( )
如图,在等腰Rt△ABC和等腰Rt△ADE中,∠BAC=∠DAE=90°,点C、D、E在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④BE2=2(AD2+AB2).其中,结论正确的个数是( ) (1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长;
(1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长; 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E.求:
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB的垂直平分线分别交AB、AC于点D、E.求: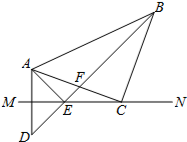 如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.
如图,已知,MN是AD的垂直平分线,点C在MN上,∠MCA=20°,∠ACB=90°,CA=CB=5,BD交MN于点E,交AC于点F,连接AE.