题目内容
16.⊙O的直径为12cm,弦AB垂直平分半径OC,则弦AB的长为6$\sqrt{3}$cm.分析 设AB交OC于点D,由垂径定理可知AD=BD,在Rt△AOD中,由勾股定理可求得AD的长,则可求得弦AB的长.
解答  解:
解:
设AB交OC于点D,由垂径定理可知AD=BD,
∵AB平分OC,且直径为12cm,
∴OC=OA=6cm,
连接OA,在Rt△AOD中,由勾股定理可得
AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$(cm),
∴AB=2AD=6$\sqrt{3}$cm,
故答案为:6$\sqrt{3}$cm.
点评 本题主要考查垂径定理的应用,掌握垂直弦的直径平分弦是解题的关键,注意构造直角三角形.

练习册系列答案
相关题目
20.任意写一个各数位上数字都不相同的三位数,用数位上的3个数字分别组成一个最大的三位数和一个最小的三位数,然后把这两个数相减,取差的绝对值,得到一个新的三位数.重复上述操作,你最后得到的数是495.
5.若x2-mx+$\frac{49}{25}$=(x+$\frac{7}{5}$)2,则m的值为( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{14}{5}$ | D. | -$\frac{14}{5}$ |
6.下列运算中,正确的是( )
| A. | a•a2=a2 | B. | (a2)2=a4 | C. | a2•a3=a6 | D. | (a2b)3=a2•b3 |
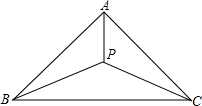 三角形ABC中,∠ABC和∠ACB的角平分线相交于点P,连接AP,若∠BPC=130°,则∠BAP=40°.
三角形ABC中,∠ABC和∠ACB的角平分线相交于点P,连接AP,若∠BPC=130°,则∠BAP=40°. 如图,用两个长为8,宽为4的矩形纸条交叉重叠地放在一起(两纸片不完全重合),重合部分是四边形ABCD,设四边形ABCD的面积为S,则S的取值范围是16≤S≤20.
如图,用两个长为8,宽为4的矩形纸条交叉重叠地放在一起(两纸片不完全重合),重合部分是四边形ABCD,设四边形ABCD的面积为S,则S的取值范围是16≤S≤20.