题目内容
7.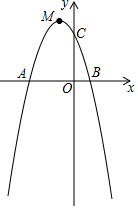 如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).
如图,抛物线与x轴交于点A(-3,0),B(1,0)两点,与y轴交于点C(0,3).(1)求此抛物线的解析式;
(2)抛物线的顶点为M,点M关于x轴的对称点为M′,直线BM′与抛物线的另一个交点为点D,求△CBD的面积;
(3)点P为x轴上方的抛物线上的一动点,过点P作y轴的平行线交直线BD于点Q,求四边形APBQ面积的最大值,并求出此时点P的坐标.
分析 (1)直接利用待定系数法求出二次函数解析式即可;
(2)首先得出M以及M′的坐标,进而求出直线BM′的解析式,再求出D点坐标,进而利用S△DBC=S△CFB+S△DFB得出答案;
(3)直接利用已知表示出四边形APBQ面积进而得出答案.
解答 解:(1)设抛物线解析式为:y=ax2+bx+c,将点A(-3,0),B(1,0),C(0,3)分别代入得:
$\left\{\begin{array}{l}{9a-3b+c=0}\\{a+b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
故抛物线解析式为:y=-x2-2x+3;
(2)如图所示:∵y=-x2-2x+3=-(x+1)2+4,
∴M(-1,4),
∴点M关于x轴的对称点为M′(-1,-4),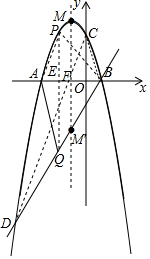
设BM′的解析式为:y=kx+d,
则$\left\{\begin{array}{l}{k+d=0}\\{-k+d=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{d=-2}\end{array}\right.$,
故BM′的解析式为:y=2x-2,
将两函数解析式联立得:
$\left\{\begin{array}{l}{y=-{x}^{2}-2x+3}\\{y=2x-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=-12}\end{array}\right.$,
即D(-5,-12),
设直线DC的解析式为:y=ex+g,
则$\left\{\begin{array}{l}{-5e+g=-12}\\{g=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{e=3}\\{g=3}\end{array}\right.$,
故直线DC的解析式为:y=3x+3,
当y=0,则x=-1,即直线DC与x轴的交点F(-1,0),
故BF=1+1=2,
则S△DBC=S△CFB+S△DFB=$\frac{1}{2}$×2×3+$\frac{1}{2}$×2×12=15;
(3)如图所示:设P(x,-x2-2x+3),则Q(x,2x-2),
四边形APBQ面积=S△APB+S△AQB=$\frac{1}{2}$×AB(-x2-2x+3)+$\frac{1}{2}$×AB×[-(2x-2)]
=2(-x2-2x+3-2x+2)
=-2x2-8x+10
=-2(x+2)2+18,
当x=-2时,S四边形APBQ最大,此时-x2-2x+3=3,
即P(-2,3).
点评 此题主要考查了二次函数综合以及二次函数最值求法、待定系数法求一次函数解析式等知识,正确分割图形求面积是解题关键.

 阅读快车系列答案
阅读快车系列答案 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=1,将△ABC绕点C顺时针旋转得△A1B1C1,且点A1落在边AB边上,取BB1的中点D,连接CD,则CD的长为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
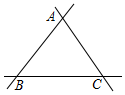 某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )| A. | 两个角的平分线的交点处 | B. | 两边高线的交点处 | ||
| C. | 两边中线的交点处 | D. | 内部即可 |
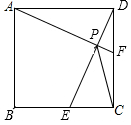 如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
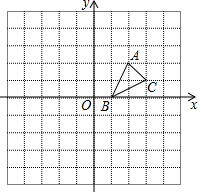 如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).
如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).