题目内容
7. y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论
y=ax2+bx+c+2的图象如图所示,顶点为(-1,0),下列结论①abc>0;②b2-4ac=0;③a>2;④4a-2b+c>0.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①首先根据抛物线开口向上,可得a>0;然后根据对称轴在y轴左边,可得b>0;最后根据抛物线与y轴的交点在x轴的上方,可得c>0,据此判断出abc>0即可.
②根据二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,可得△=0,即b2-4a(c+2)=0,b2-4ac=8a>0,据此解答即可.
③首先根据对称轴x=-$\frac{b}{2a}$=-1,可得b=2a,然后根据b2-4ac=8a,确定出a的取值范围即可.
④根据对称轴是x=-1,而且x=0时,y>2,可得x=-2时,y>2,据此判断即可.
解答 解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c+2>2,
∴c>0,
∴abc>0,
∴结论①正确;
∵二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,
∴△=0,
即b2-4a(c+2)=0,
∴b2-4ac=8a>0,
∴结论②不正确;
∵对称轴x=-$\frac{b}{2a}$=-1,
∴b=2a,
∵b2-4ac=8a,
∴4a2-4ac=8a,
∴a=c+2,
∵c>0,
∴a>2,
∴结论③正确;
∵对称轴是x=-1,而且x=0时,y>2,
∴x=-2时,y>2,
∴4a-2b+c+2>2,
∴4a-2b+c>0.
∴结论④正确.
综上,可得
正确结论的个数是3个:①③④.
故选C.
点评 本题主要考查了二次函数的图象与系数的关系,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案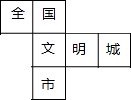 在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )
在市委、市政府的领导下,全市人民齐心协力,力争于2017年将我市创建为“全国文明城市”,为此小宇特制了正方体模具,其展开图如图所示,原正方体中与“文”字所在的面正对面上标的字是( )| A. | 全 | B. | 国 | C. | 明 | D. | 城 |
| A. | x2+2x=x2-1 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |
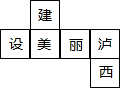 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 泸 | D. | 西 |
| A. | 8 | B. | 7 | C. | 8或7 | D. | 9或8 |
| A. | 35° | B. | 110° | C. | 35°或145° | D. | 35°或140° |
 如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )
如图,AB∥CD,AD=CD,∠1=70°30',则∠2的度数是( )| A. | 40°30' | B. | 39°30' | C. | 40° | D. | 39° |
| A. | 正方形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 钝角三角形 |
| A. | a是无理数 | B. | a是方程x2-3=0的解 | ||
| C. | a是8的算术平方根 | D. | 2<a<4 |