题目内容
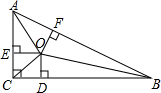 如图,在△ABC中,∠ACB=90°,点O为三角形三个内角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,CB=8cm,CA=6cm,求OD的长.
如图,在△ABC中,∠ACB=90°,点O为三角形三个内角平分线的交点,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,且AB=10cm,CB=8cm,CA=6cm,求OD的长.考点:角平分线的性质
专题:
分析:根据角平分线性质求出OD=OE=OF,根据三角形的面积公式得出
×AC×BC=
×AC×R+
×BC×R+×AB×R,代入求出即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵点O为三角形三个内角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,
∴OD=OE=OF,
设OD=OE=OF=R,
由三角形的面积公式得:S△ACB=S△AOC+S△AOB+S△BOC,
×AC×BC=
×AC×R+
×BC×R+×AB×R,
6×8=6R+8R+10R,
R=2,
即OD=2cm.
∴OD=OE=OF,
设OD=OE=OF=R,
由三角形的面积公式得:S△ACB=S△AOC+S△AOB+S△BOC,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
6×8=6R+8R+10R,
R=2,
即OD=2cm.
点评:本题考查了对角的平分线性质和三角形的面积的应用,注意:角平分线上的点到角的两边的距离相等.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
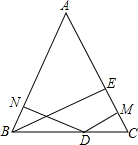 如图所示,∠B=∠C,BE⊥AC,DM⊥AC,DN⊥AB,求证:DM+DN=BE.
如图所示,∠B=∠C,BE⊥AC,DM⊥AC,DN⊥AB,求证:DM+DN=BE. 小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度.
小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度.