题目内容
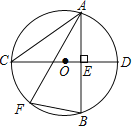
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]() ,垂足为
,垂足为![]() ,
,![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,连结
的中点,连结![]() ,过点
,过点![]() 作直线
作直线![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求⊙
,求⊙![]() 的半径
的半径
【答案】(1)见解析;(2)2
【解析】
(1)连接OE,OF,利用垂径定理及等腰三角形的性质得到∠DOF=∠DOE.而∠DOE=2∠A,所以![]() ,由
,由 ![]() 得到
得到![]() ,
,
于是可求出![]() ,所以
,所以![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接OM,如图,利用圆周角定理得到∠AEB=90°.再证明OM∥AE得到∠MOB=∠A=30°.而∠DOF=2∠A=60°,所以∠MOF=90°,设⊙O的半径为r,利用含30度的直角三角形三边的关系得OM,然后根据勾股定理列出方程求解即可.
解:(1)如图,连结![]() ,
,![]() ,
,

∵![]() ,
,![]() 是⊙
是⊙![]() 的直径
的直径
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 为⊙
为⊙![]() 的切线
的切线
(2)连接![]() ,
,

∵![]() 为⊙
为⊙![]() 的直径,
的直径,
∴![]() 为
为![]() 中点,
中点,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,![]()
设⊙![]() 的半径为
的半径为![]() .
.
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∵![]()
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
解得![]() .(舍去负根)
.(舍去负根)
∴⊙![]() 的半径为2.
的半径为2.

练习册系列答案
相关题目