Question

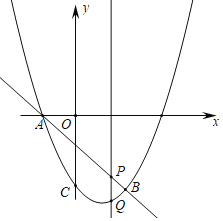
【题目】已知抛物线C：y1＝ax2－ah(2x－h)－2，直线l：y2＝k(x－h)－2．

(1)求证：直线l恒过抛物线C的顶点；

(2)当a＝－1，m≤x≤2时，y1≥x－4恒成立，求m的最小值；

(3)当0＜a≤3，k＞0时，若在直线l下方的抛物线C上至少存在两个横坐标为整数的点，求k的取值范围．

Answer 1

【答案】（1）证明见解析；（2）1；（3）k＞6．

【解析】

(1)由抛物线的解析式可知抛物线的顶点坐标为(h，-2)，然后证明点(h,-2)符合直线y2＝k(x－h)－2的解析式即可;

(2)令,依据拋物线的解析式可得到拋物线的顶点在直线y=-2上，由m≤x≤2时，y1≥x－4恒成立可得到拋物线的顶点坐标为(2，-2)，然后找出抛物线y1＝ax2－ah(2x－h)－2位于直线上方时自变量x的取值范围，从而可确定出m的最小值;

(3)由(1)可知抛物线C与直线l都过点A(h,-2).当0<a≤3时，k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点，即当x=h+2时，恒成立，然后由可得到关于k的不等式，从而可求得k:的取值范围.

解：(1)y1＝ax2－ah(2x－h)－2=

抛物线C的顶点坐标为(h,-2)，当x=h时,y2＝k(h－h)－2=-2，所以直线l恒过抛物线C的顶点（h,-2）;

(2)当a=-1时,抛物线C解析式为y1=，令如图所示:

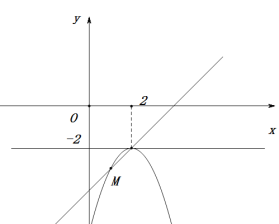
抛物线C的顶点在直线y=-2上移动,图1当m≤x≤2时,y1≥x－4恒成立，则可知抛物线C的顶点为(2,-2)，设抛物线C与直线除顶点外的另一交点为M,此时点M的横坐标即为m的最小值,由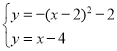，解得,所以m的最小值为1.

(3)如图2所示:由(1)可知:抛物线C与直线l都过点A(h,-2).如图所示：

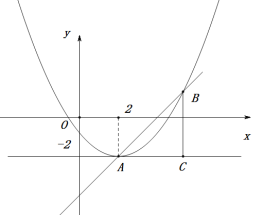
当0<a≤3时,k>0,在直线l下方的抛物线C上至少存在两个横坐标为整数点,即当x=h+2时,恒成立.

所以，整理得：得:k>2a.又因为0<a≤3，所以0<2a<6，所以k>6.

分析: