题目内容
【题目】已知:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() ,
,![]() ,连接
,连接![]() .
.
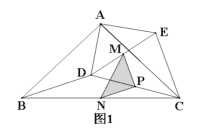

(1)如图1所示,线段![]() 与
与![]() 的数量关系是_____,位置关系是_____;
的数量关系是_____,位置关系是_____;
(2)在图1中,若点M、P、N分别为![]() 的中点,连接
的中点,连接![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)如图2所示,若M、N、P分别为![]() 上的点,且满足
上的点,且满足![]() ,
,![]() ,连接
,连接![]() ,则线段
,则线段![]() 长度是多少?
长度是多少?
【答案】(1)相等,垂直;(2)![]() 为等腰直角三角形,证明见解析;(3)
为等腰直角三角形,证明见解析;(3)![]() .
.
【解析】
(1)延长BD与EC相交于F,证明△ABD≌△ACE,根据全等三角形的性质可得BD=CE,![]() ,再进一步证明
,再进一步证明![]() 可得∠BFC=90°,由此可证明
可得∠BFC=90°,由此可证明![]() 与
与![]() 垂直且相等;
垂直且相等;
(2)结合(1),根据中位线的定理,可推出![]() 为等腰直角三角形;
为等腰直角三角形;
(3)证明△CPN∽△CDB,△DPM∽△DCE,根据相似三角形的性质可求得NP和MP的值,结合(2)可证明∠NPM=90°,根据勾股定理可求得MN的长度.
解:(1)如下图延长BD与EC相交于F,
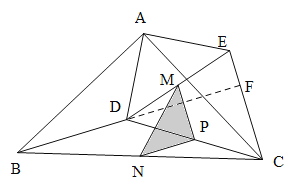
∵![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,
∴![]()
∴![]()
又∵![]() ,
,![]()
∴△ABD≌△ACE(SAS)
∴BD=CE,![]() ,
,
∵![]()
∴![]() ,
,
∴ ![]()
∴![]() ,即
,即![]()
∴![]() ,即
,即![]() .
.
故线段![]() 与
与![]() 的数量关系是相等,位置关系是垂直.答案为:相等,垂直.
的数量关系是相等,位置关系是垂直.答案为:相等,垂直.
(2)![]() 为等腰直角三角形,理由如下:
为等腰直角三角形,理由如下:
∵点M、P、N分别为![]() 的中点,
的中点,
∴NP和MP分别为△BCD和△ECD的中位线,
∴![]()
∴![]() ,
,
由(1)得BD=CE,
∴![]() ,
,
由(1)得![]() ,
,
∴![]()
∴![]() ,即
,即![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
(3)∵![]()
∴![]()
又∵∠BCD=∠BCD
∴△CPN∽△CDB
∴![]() ,
,![]() ,
,
∴NP//BD,
∵![]()
∴![]() ,
,
同理可证△DPM∽△DCE,![]() ,MP//EC,
,MP//EC,
∴![]()
与(2)同理可证![]() ,
,
∴在Rt△![]() 中,根据勾股定理
中,根据勾股定理
![]() .
.

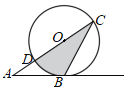
【题目】如图,⊙O的圆心O在△ABC的边AC上,AC与⊙O分别交于C,D两点,⊙O与边AB相切,且切点恰为点B.
(1)求证:∠A+2∠C=90°;
(2)若∠A=30°,AB=6,求图中阴影部分的面积.
【题目】某商业集团新进了40台空调机,60台电冰箱,计划调配给下属的甲、乙两个连锁店销售,其中70台给甲连锁店,30台给乙连锁店.两个连锁店销售这两种电器每台的利润(单位:元)如下表:
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店![]() 台空调机,集团卖出这100台电器的总利润为
台空调机,集团卖出这100台电器的总利润为![]() (元).
(元).
(1)求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)为了促销,集团决定仅对甲连锁店的空调机每台让利![]() 元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.
元销售,其他的销售利润都不变,并且让利后每台空调机的利润比甲连锁店销售每台电冰箱的利润至少高出10元,问该集团应该如何设计调配方案,能使总利润达到最大.