题目内容
△ABC的内切圆⊙O与AC、AB、BC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,求AE、BF和CD的长.
考点:三角形的内切圆与内心
专题:计算题
分析:先根据切线长定理得到AE=AD,BE=BF,CF=CD,设AE=x,则AD=x,BE=BF=5-x,CD=CF=6-x,则利用BC的长列方程得到5-x+6-x=9,解得x=1,然后计算BF和CD的长.
解答:解: 如图,
如图,
∵△ABC的内切圆⊙O与AC、AB、BC分别相切于点D、E、F,
∴AE=AD,BE=BF,CF=CD,
设AE=x,则AD=x,BE=AB-AE=5-x,CD=AC-AD=6-x,
∴BF=5-x,CF=6-x,
∴5-x+6-x=9,解得x=1,
∴AE=1,BF=5-x=4,CD=6-x=5,
即AE、BF和CD的长分别为1,4,5.
 如图,
如图,∵△ABC的内切圆⊙O与AC、AB、BC分别相切于点D、E、F,
∴AE=AD,BE=BF,CF=CD,
设AE=x,则AD=x,BE=AB-AE=5-x,CD=AC-AD=6-x,
∴BF=5-x,CF=6-x,
∴5-x+6-x=9,解得x=1,
∴AE=1,BF=5-x=4,CD=6-x=5,
即AE、BF和CD的长分别为1,4,5.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
下列由左边到右边的变形中,是因式分解的是( )
| A、(x+2)(x-2)=x2-4 | ||
| B、x2-4=(x+2)(x-2) | ||
| C、x2-4+3x=(x+2)(x-2)+3x | ||
D、x2-1=x(x-
|
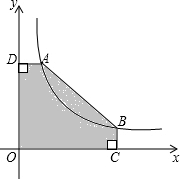 如图,A(2,m),B(6,n)是双曲线y=
如图,A(2,m),B(6,n)是双曲线y=



 如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3).
如图,抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3).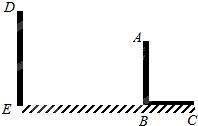 已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.