题目内容
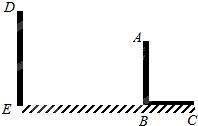 已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.
已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m.(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长.
考点:平行投影
专题:计算题
分析:(1)根据太阳光线为平行光线,连结AC,然后过D点作AC的平行线交BC于E即可;
(2)证明△ABC∽△DEF,利用相似比计算DE的长.
(2)证明△ABC∽△DEF,利用相似比计算DE的长.
解答:解:(1)(连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影,如图;
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴
=
,即
=
∴DE=12(m).
(2)∵AC∥DF,

∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°,
∴△ABC∽△DEF,
∴
| AB |
| DE |
| BC |
| EF |
| 6 |
| DE |
| 3 |
| 6 |
∴DE=12(m).
点评:本题考查了平平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.

练习册系列答案
相关题目
若方程3(2x-2)=9-3x的解与关于x的方程6-2k=2(x+3)的解相同,则实数k的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
 小红第1至6周每周零花钱收支情况如图所示,6周后小红的零花钱一共还剩
小红第1至6周每周零花钱收支情况如图所示,6周后小红的零花钱一共还剩 反比例函数y=
反比例函数y= 如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.
如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.