题目内容
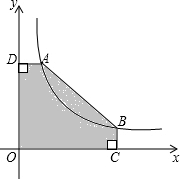 如图,A(2,m),B(6,n)是双曲线y=
如图,A(2,m),B(6,n)是双曲线y=| 12 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:可先求得A、B的坐标,过点A作AE⊥x轴于点E,可分别计算矩形AEOD和梯形ABCE的面积,可求得五边形ABCOD的面积.
解答:解:∵A(2,m),B(6,n)是双曲线y=
上两点,
∴2m=12,6n=12,解得m=2,n=6,
∴A(2,6),B(6,2),
过A作AE⊥x轴于点E,
则AD=OE=2,AE=OD=6,BC=2,OC=6,CE=OC-OE=6-2=4,
∴S五边形ABCOD=S矩形AEOD+S梯形ABCE=OE•OD+
(BC+AE)•CE=2×6+
×(2+6)×4=28.
| 12 |
| x |
∴2m=12,6n=12,解得m=2,n=6,
∴A(2,6),B(6,2),
过A作AE⊥x轴于点E,
则AD=OE=2,AE=OD=6,BC=2,OC=6,CE=OC-OE=6-2=4,
∴S五边形ABCOD=S矩形AEOD+S梯形ABCE=OE•OD+
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查反比例函数图象上点的特征,求得A、B两点的坐标得到相应线段的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,在墙角B处有一只猫,通过挂在墙CD上点O处的一平面镜正好看到另一房间A处有一只老鼠在偷吃东西.已知A点和B点均距挂镜子的墙CD=4米,A、B两点距离是6米.若猫去捉老鼠必经过O点处的门口(不计门口宽度),请你猜测猫从B点到A点至少要经过多少米的路程?
如图所示,在墙角B处有一只猫,通过挂在墙CD上点O处的一平面镜正好看到另一房间A处有一只老鼠在偷吃东西.已知A点和B点均距挂镜子的墙CD=4米,A、B两点距离是6米.若猫去捉老鼠必经过O点处的门口(不计门口宽度),请你猜测猫从B点到A点至少要经过多少米的路程?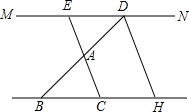 已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.

 如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.
如图,在△ABC中,点O是边AC上的一个动点,过O点作直线MN∥BC,设MN交∠ACB的角平分线于点E,交∠ACB外角的平分线于点F.