题目内容
19.某公园的门票价格规定如表:| 购票人数 | 1~50人 | 51~100人 | 100以上 |
| 票价 | 10元/人 | 8元/人 | 5元/人 |
(2)若有A、B两个团队共160人,以各自团队为单位分别买票,共用950元,问A、B两个团队各有多少人?
分析 (1)本题等量关系有:甲班人数×8+乙班人数×10=920;(甲班人数+乙班人数)×5=515,据此可列方程组求解;
(2)A团队a人,B团队(160-a)人,根据收费标准进行分类讨论,并列出方程进行解答.
解答 解:(1)设甲班有x人,乙班有y人.
由题意得:$\left\{\begin{array}{l}{8x+10y=920}\\{5(x+y)=515}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=55}\\{y=48}\end{array}\right.$.
答:甲班55人,乙班48人;
(2)设A团队a人,B团队(160-a)人,
①当1<a≤50时,由题意得:10a+5(160-a)=950,
解得a=10,
则160-a=150.
即A团队10人,B团队150人;
②当51<a≤100时,由题意得:8a+10(160-a)=950,
解得a=325,不合题意,舍去.
综上所述,A团队10人,B团队150人.
点评 本题考查了二元一次方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.本题按购票人数分为三类门票价格.

练习册系列答案
相关题目
9.下列语句中,正确的是( )
| A. | 相等的角一定是对顶角 | |
| B. | 垂线最短 | |
| C. | 过一点有且只有一条直线与已知直线垂直 | |
| D. | 有一个公共顶点,且两边互为反向延长线的两个角是对顶角 |
7.三元一次方程组$\left\{\begin{array}{l}{2x-3y+2z=5}\\{x-2y+3z=-6}\\{3x-y+z=3}\end{array}\right.$ 消去未知数y后,得到的方程组可能是( )
| A. | $\left\{\begin{array}{l}{7x+z=4}\\{5x-z=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7x+z=4}\\{x-5z=8}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{7x-z=12}\\{x-5z=28}\\{\;}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x-z=4}\\{x-5z=12}\end{array}\right.$ |
14. 如图,已知∠1=∠2,则下列结论一定正确的是( )
如图,已知∠1=∠2,则下列结论一定正确的是( )
 如图,已知∠1=∠2,则下列结论一定正确的是( )
如图,已知∠1=∠2,则下列结论一定正确的是( )| A. | ∠3=∠4 | B. | AB∥CD | C. | AD∥BC | D. | ∠B=∠D |
4.201718的个位上的数字是( )
| A. | 7 | B. | 3 | C. | 9 | D. | 1 |
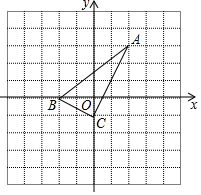 如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)
如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)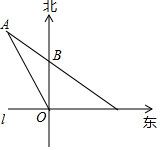 如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.
如图,在东西方向的海岸线上有一个码头M,在码头M的正西方向有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距60$\sqrt{3}$千米的A处;经过3小时,又测得该轮船位于O的正北方向,且与O相距60千米的B处.