题目内容
10.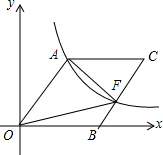 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),与BC交于点F,则△AOF的面积等于( )| A. | 50 | B. | 40 | C. | 30 | D. | 20 |
分析 连接AB,过点A作AD⊥x轴于点D,根据菱形的性质即可得出OA∥BC、OB=OA,由△AOF和△AOB有共同的底OA结合平行线的性质即可得出S△AOF=S△AOB,再根据点A的横坐标结合反比例函数图象上点的坐标特征即可得出点A的坐标,进而得出OB、AD的长度,利用三角形的面积公式即可求出S△AOB的值,此题得解.
解答 解:连接AB,过点A作AD⊥x轴于点D,如图所示.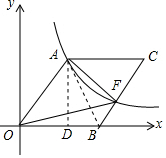
∵四边形OACB是菱形,
∴OA∥BC,OB=OA,
又∵△AOF和△AOB有共同的底OA,
∴S△AOF=S△AOB.
∵反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A(6,m),
∴6m=48,m=8,
∴OB=OA=$\sqrt{{6}^{2}+{8}^{2}}$=10,AD=8,
∴S△AOF=S△AOB=$\frac{1}{2}$OB•AD=$\frac{1}{2}$×10×8=40.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征、菱形的性质以及三角形的面积,根据面积法找出S△AOF=S△AOB是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
5. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | cosC=$\frac{CD}{AC}$ | B. | cosC=$\frac{AC}{BC}$ | C. | cosC=$\frac{AD}{AC}$ | D. | cosC=$\frac{AD}{AB}$ |
2.下列各式不能因式分解的是( )
| A. | a2-b2 | B. | a2-2a+1 | C. | ab-a | D. | a2+b2 |
19.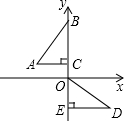 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| B. | △ABC绕点C逆时针旋转90°,再向下平移3 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C顺时针旋转90°,再向下平移3 |
 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线AD交BC于点D,若DE垂直平分AB,交AB于点E,则∠B=30°. 某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)
某校王老师组织九(1)班同学开展数学活动,某天带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A的仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高AB.(结果用根号表示)