题目内容
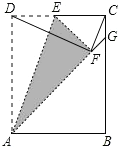 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G,连接EG、DF、CF.
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G,连接EG、DF、CF.(1)△AEG、△DFC是直角三角形;(2)EG∥DF;(3)CG=
| 1 |
| 4 |
| CG |
| BG |
| AD |
| AB |
| ||
| 2 |
上述说法正确的有( )个.
| A、4 | B、3 | C、2 | D、1 |
考点:翻折变换(折叠问题)
专题:
分析:连接EG,如图,根据折叠的性质得ED=EF,∠AED=∠AEF,∠AFE=∠ADE=90°,由ED=EC得到EC=EF,则利用“HL”可判断Rt△EGF≌Rt△EGC,则∠CEG=∠FEG,于是有∠AEG=
∠DEF+
∠CEF=90°,即△AEG为直角三角形;由于EF=ED=EC,根据圆周角定理的推论得△DFC为直角三角形,则可对(1)进行判断;根据折叠得到DF⊥AE,而EG⊥AE,根据平行线的判定得到EG∥DF,于是可对(2)进行判断;由Rt△EGF≌Rt△EGC得CG=FG,设CG=k,BG=1,则AD=BC=k+1,FG=k,利用折叠的性质得AF=AD=k+1,则AG=AF+FG=2k+1,在Rt△ABG中,根据勾股定理计算出AB=2
,则
=
,则可对(4)进行判断;由于只有当k=
时,即
=
,才有CG=
BC=
AD,由此可对(3)进行判断.
| 1 |
| 2 |
| 1 |
| 2 |
| k2+k |
| AD |
| AB |
| ||
2
|
| 1 |
| 3 |
| CG |
| BG |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:连接EG,如图,
∵△ADE沿AE折叠后得到△AFE,
∴ED=EF,∠AED=∠AEF,∠AFE=∠ADE=90°,
∵ED=EC,
∴EC=EF,
在Rt△EGF和Rt△EGC中
,
∴Rt△EGF≌Rt△EGC,
∴∠CEG=∠FEG,
∴∠AEG=
∠DEF+
∠CEF=
×180°=90°,
∴△AEG为直角三角形;
∵EF=ED=EC,
∴△DFC为直角三角形,所以(1)正确;
∵∠AEG=90°,
∴EG⊥AE,
∵△ADE沿AE折叠后得到△AFE,
∴DF⊥AE,
∴EG∥DF,所以(2)正确;
∵Rt△EGF≌Rt△EGC,
∴CG=FG,
设CG=k,BG=1,则BC=k+1,FG=k,
∴AD=k+1,
∵△ADE沿AE折叠后得到△AFE,
∴AF=AD=k+1,
∴AG=AF+FG=2k+1,
在Rt△ABG中,
AB=
=
=2
,
∴
=
=
,所以(4)错误;
当k=
时,即
=
时,CG=
BC=
AD,所以(3)错误.
故选:B.
∵△ADE沿AE折叠后得到△AFE,
∴ED=EF,∠AED=∠AEF,∠AFE=∠ADE=90°,
∵ED=EC,
∴EC=EF,
在Rt△EGF和Rt△EGC中
|
∴Rt△EGF≌Rt△EGC,
∴∠CEG=∠FEG,
∴∠AEG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴△AEG为直角三角形;
∵EF=ED=EC,
∴△DFC为直角三角形,所以(1)正确;

∵∠AEG=90°,
∴EG⊥AE,
∵△ADE沿AE折叠后得到△AFE,
∴DF⊥AE,
∴EG∥DF,所以(2)正确;
∵Rt△EGF≌Rt△EGC,
∴CG=FG,
设CG=k,BG=1,则BC=k+1,FG=k,
∴AD=k+1,
∵△ADE沿AE折叠后得到△AFE,
∴AF=AD=k+1,
∴AG=AF+FG=2k+1,
在Rt△ABG中,
AB=
| AF2-BG2 |
| (2k+1)2-12 |
| k2+k |
∴
| AD |
| AB |
| k+1 | ||
2
|
| ||
2
|
当k=
| 1 |
| 3 |
| CG |
| BG |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
故选:B.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质、圆周角定理的推论和三角形全等的判定与性质.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
如果方程组
的解中的x与y的值相等,那么a的值是( )
|
| A、1 | B、2 | C、3 | D、4 |
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
下列运算正确的是( )
| A、3x3-5x3=-2 |
| B、(6x3)÷(2x2)=3x(x≠0) |
| C、(x3)2=x5 |
| D、-3x(2x-4)=-6x2-12x |
下列计算结果正确的是( )
| A、(2x5)3=6x15 |
| B、(-x4)3=-x12 |
| C、(2x3)2=2x6 |
| D、[(-x)3]4=x7 |
 如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:
如图,正方形OABC与正方形ODEF是位似图形,O为位似中心,相似比为1:| 2 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
| D、(-2,-2) |
 如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为
如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为