题目内容
13.中国移动通讯公司推出动感地带、神州行和全球通三种业务品牌,在平江县的资费标准如下:注:(3)问是附加题,可以不做,总分不超过120分| 品牌类型 | 月租费(元) | 必选业务套餐费(元) | 本地通话费(元/分钟) | 长途通话费(元/分钟) |
| 动感地带 | 0 | 18 | 0.3 | 0.6 |
| 神州行 | 10 | 5 | 0.4 | 0.6 |
| 全球通 | 0 | 68 | 1~288分钟免费,超过288分钟 0.2元/分钟(不区分长途通话和本地通话) | |
(2)现在移动公司又推出了新的两项优惠活动:优惠活动一,1元绑定亲情号码,给亲情号码打电话免费.动感地带最多可以绑定1个,神州行最多可以绑定2个,全球通最多可以绑定3个亲情号码;优惠活动二,集团业务每月5元,集团网内部通话免费.那么小明参加优惠活动吗?如果小明参加优惠活动,参加活动后比原来节约多少话费?(假如小明的朋友都加入了平江县的某集团网,两项优惠活动可以同时参加).
分析 (1)分别求得三种情况下所缴纳的话费,通过比较可得问题答案;
(2)根据题意可以分别求出三种情况下所缴纳的费用,通过比较可以得到选择哪种品牌的电话卡,同时可以计算出节省多少费用.
解答 解:(1)根据题意可得,
当小明选择动感地带时,18+0.6×2×60+0.3×1×60=108元;
当小明选择神州行时,10+5+0.6×2×60+0.4×1×60=111元;
当小明选择全球通时,(1+2)×60=180<288,缴纳的话费为68元;
∵68<108<111,
∴小明选择全球通最省钱.
即开通全球通品牌的业务才能最省钱.
(2)当小明选择动感地带时,小明两项活动都参加,则花费为18+1+5=24元;
当小明选择神州行时,小明两项活动都参加,则花费为:10+5+1+5=21元;
当选择全球通时,因为时间够用,不用选择优惠活动;
由上可得,小明参加优惠活动,且选择神州行,节约的话费为:68-21=47元,
即小明参加优惠活动,且选择神州行,节约的话费是47元.
点评 本题考查有理数的混合运算,解题的关键是能看懂题意,根据表格中的数据能计算出选择不同的品牌电话卡,所缴纳的电话费不一样.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.菱形具有而矩形不一定具有的性质是( )
| A. | 两条对角线相等 | B. | 两条对角线互相垂直 | ||
| C. | 两条对角线互相平分 | D. | 两组对边分别相等 |
3.圆的周长是2π,如果一条直线与圆心的距离是$\frac{π}{2}$,那么这条直线与这个圆的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 不能确定 |
 画出下列△ABC关于直线l的轴对称图形.
画出下列△ABC关于直线l的轴对称图形.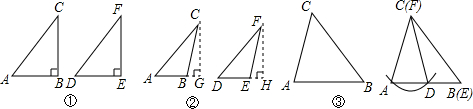
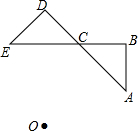 如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.
如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.