题目内容
9.解方程:(1)x2+2x-5=0;
(2)x(x-8)=16
(3)(x-2)2-4=0.
分析 (1)把常数项5移项后,应该在左右两边同时加上一次项系数2的一半的平方.
(2)先把方程化为一般式,然后利用配方法解方程.
(3)先移项,把方程变为(x+a)2=b(b≥0)的形式,用直接开平方法进行解答.
解答 解:(1)∵x2+2x-5=0,
∴x2+2x=5,
∴x2+2x+1=5+1,
∴(x+1)2=6,
∴x+1=±$\sqrt{6}$,
∴x=-1±$\sqrt{6}$;
(2)由原方程得到:x2-8x=16,
x2-8x+16=32,
(x-4)2=32,
所以x1=4+4$\sqrt{2}$,x2=4-4$\sqrt{2}$;
(3)∵(x-2)2-4=0.即(x-2)2=4
∴x-2=±2
∴x1=4,x2=0.
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列函数中,为一次函数的是( )
| A. | $y=\frac{1}{x}+1$ | B. | y=-2x | C. | y=x2+1 | D. | y=kx+1(k是常数) |
14. 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )| A. | 外心 | B. | 内心 | C. | 重心 | D. | 无法确定 |
 在图的方格纸中画出△ABC关于y轴对称的图形.
在图的方格纸中画出△ABC关于y轴对称的图形.
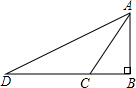 如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为30°,沿AE方向前进100米到达点C处,测得建筑物的顶端A的仰角为45°,求建筑物的高.
如图,某人要测一建筑物AB的高度,他在地面D处测得建筑物顶端A的仰角为30°,沿AE方向前进100米到达点C处,测得建筑物的顶端A的仰角为45°,求建筑物的高.