题目内容
13.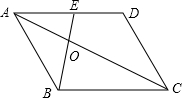 如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.
如图,在?ABCD中,点E是AD的中点,连接AC、BE相交于点O,则S△AOE:S△AOB=$\frac{1}{2}$.
分析 根据平行四边形的性质得到AD=BC,AD∥BC,由点E是AD的中点,得到AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,通过△AOE∽△BCO,根据相似三角形的性质得到$\frac{OE}{BO}=\frac{AE}{BC}=\frac{1}{2}$,于是得到结论.
解答 解:在?ABCD中,
∵AD=BC,AD∥BC,
∵点E是AD的中点,
∴AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∵AD∥BC,
∴△AOE∽△BCO,
∴$\frac{OE}{BO}=\frac{AE}{BC}=\frac{1}{2}$,
∴S△AOE:S△AOB=$\frac{OE}{BO}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度不大,注意掌握相似三角形面积的比等于相似比的平方定理的应用是解此题的关键.

练习册系列答案
相关题目
3.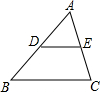 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
 如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )
如图,DE是△ABC的一条中位线,若△ADE的面积为2,则四边形DBCE的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
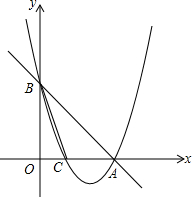 已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.
已知:如图直线y=-x+6与x轴、y轴分别交于A、B两点.抛物线y=$\frac{1}{2}$x2+bx+c过A、B两点,与x轴的另一个交点为C点.
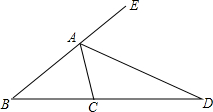 如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.
如图,已知△ABC中,AD是△ABC外角平分线,交BC延长线于D,求证:$\frac{AB}{AC}$=$\frac{BD}{DC}$.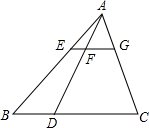 如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.
如图,在△ABC中,点D在BC上,EG∥BC分别交AB,AD,AC于点E,F,G.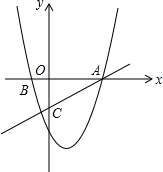 如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.
如图.在平面直角坐标系xOy中,抛物线y=x2-2x-3交x轴于A、B两点,直线y=$\frac{1}{3}$x-1交y轴于点C,若x轴上的点P满足PA=PC,则P点坐标为($\frac{4}{3},0$);若在抛物线对称轴上且位于x轴上方的点Q满足∠OAC<∠QCA<3∠OAC,则点Q纵坐标y取值范围为$0<y<\frac{17}{7}$.