题目内容
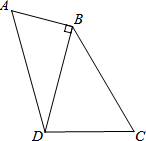 如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.
如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.考点:解直角三角形
专题:
分析:过点D作DE⊥BC于点E.先解直角△ABD,得出BD=AB×tan60°=2
,再解等腰直角三角形DBE,得出BE=DE=BD×sin45°=
,再解直角△CDE,
得出CE=
=
,则根据BC=BE+CE即可求解.
| 3 |
| 6 |
得出CE=
| DE |
| tan60° |
| 2 |
解答: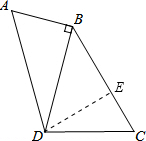 解:过点D作DE⊥BC于点E.
解:过点D作DE⊥BC于点E.
∵DB⊥AB,AB=2,∠A=60°,
∴BD=AB×tan60°=2
.
∵∠DBC=45°,DE⊥BC,
∴BE=DE=BD×sin45°=
.
∵∠C=∠A=60°,∠DEC=90°,
∴CE=
=
,
∴BC=
+
.
 解:过点D作DE⊥BC于点E.
解:过点D作DE⊥BC于点E.∵DB⊥AB,AB=2,∠A=60°,
∴BD=AB×tan60°=2
| 3 |
∵∠DBC=45°,DE⊥BC,
∴BE=DE=BD×sin45°=
| 6 |
∵∠C=∠A=60°,∠DEC=90°,
∴CE=
| DE |
| tan60° |
| 2 |
∴BC=
| 2 |
| 6 |
点评:本题考查了解直角三角形,难度适中.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
相关题目
在函数y=
的图象上,有三个点(1,y1),(
,y2),(-3,y3),则y1,y2,y3的大小关系为( )
| 1 |
| x |
| 1 |
| 2 |
| A、y1<y2<y3 |
| B、y3<y2<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
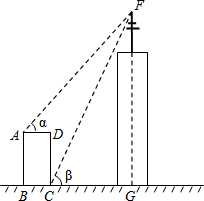 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20m,高度DC=33m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A、C两点处测得该塔顶端F的仰角分别为∠α=48°,∠β=65°,矩形建筑物宽度AD=20m,高度DC=33m.计算该信号发射塔顶端到地面的高度FG(结果精确到1m).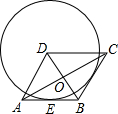 如图,在菱形ABCD中,AB=2
如图,在菱形ABCD中,AB=2