题目内容
11.如图,是由边长为1的正方形构成的网格,线线的交点叫格点,顶点在格点的三角形叫格点三角形(如△AMQ)(1)将△AMQ沿MN向右平移,使点A至点N,画出图形,并直接写出△AMQ在平移过程中覆盖的面积7.5平方单位;(2)画出△AMQ关于NQ对称的三角形;
(3)在此网格中共有6个格点三角形与△AMQ关于某条直线对称.
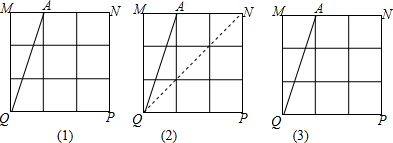
分析 (1)首先确定M、Q平移后的位置,再连接即可,然后再利用平行四边形的面积公式计算出平移过程中覆盖的面积;
(2)首先确定M、Q、N关于NQ对称的对称点的位置,再连接即可;
(3)通过变换对称轴的位置,确定对称格点三角形的个数.
解答 解:(1)如图所示:△AMQ沿MN向右平移到△M′NQ′的位置,
平移过程中覆盖的面积:2×3+$\frac{1}{2}$×1×3=7.5,
故答案为:7.5;
(2)如图:△AMQ关于NQ对称的三角形是△DPQ;
(3)在此网格中与△AMQ关于某条直线对称的格点三角形有:
△EMN,△AHL,△HNP,△KPQ,△MAC,△MCQ共6个,
故答案为:6.
点评 此题主要考查了作图--轴对称变换,以及平移变换,关键是确定组成图形的关键点的对称点和对应点的位置.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
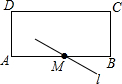 如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm.
如图所示,在矩形ABCD中,AD=4cm,AB=10cm,点M是AB边上的中点,将点A沿着过点M的直线l翻折使点A落在DC边上,点A的对称点为点P,则PD=2cm或8cm. 如图,点P是反比例函数y=-$\frac{2}{x}$图象上一点,PM⊥x轴于M,则△POM的面积为1.
如图,点P是反比例函数y=-$\frac{2}{x}$图象上一点,PM⊥x轴于M,则△POM的面积为1. 如图,△ABO≌△CDO,点E、F在线段AC上,且AF=CE.求证:FD=BE.
如图,△ABO≌△CDO,点E、F在线段AC上,且AF=CE.求证:FD=BE.