题目内容
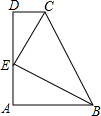如图，CD∥AB，CE平分∠BCD，BE平分∠ABC，过点E作直线垂直CD于点D，交AB于点A，则下列关系式中成立的有（ ）①
| CD |
| AD |
| DE |
| AE |
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
| A、2个 | B、3个 | C、4个 | D、5个 |
考点：相似三角形的判定与性质
专题：
分析：如图，作辅助线；首先证明∠BEC=90°；运用勾股定理证明CD=CF，BA=BF；由射影定理证明CE2=CD•BC；BE2=AB•BC，得到④成立，⑤不成立；证明△DCE∽△AEB，得到
=
，
=
，故①不成立，②、③成立．
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
解答：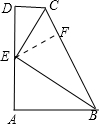
解：如图，过点E作EF⊥BC于点F；
∵CD∥AB，CE平分∠BCD，BE平分∠ABC，
∴∠DCE=∠FCE（设为α），∠ABE=∠FBE（设为β），
且2α+2β=180°，
∴α+β=90°，∠BEC=180°-90°=90°；
∵AD⊥DC，DC∥AB，
∴AD⊥AB；而CE平分∠BCD，BE平分∠ABC，
∴ED=EF，EA=EF；由勾股定理得：
CD=CF，BA=BF；由射影定理得：
CE2=CF•BC，BE2=BF•BC，
∴CE2=CD•BC；BE2=AB•BC，
∴④成立，⑤不成立；
∵∠D=∠BEC=90°，
∴∠DCE+∠DEC=∠DEC+∠AEB，
∴∠DCE=∠AEB，而∠D=∠A，
∴△DCE∽△AEB，
∴
=
，
=
，
∴①不成立，②、③成立，
故选B．
解：如图，过点E作EF⊥BC于点F；∵CD∥AB，CE平分∠BCD，BE平分∠ABC，
∴∠DCE=∠FCE（设为α），∠ABE=∠FBE（设为β），
且2α+2β=180°，
∴α+β=90°，∠BEC=180°-90°=90°；
∵AD⊥DC，DC∥AB，
∴AD⊥AB；而CE平分∠BCD，BE平分∠ABC，
∴ED=EF，EA=EF；由勾股定理得：
CD=CF，BA=BF；由射影定理得：
CE2=CF•BC，BE2=BF•BC，
∴CE2=CD•BC；BE2=AB•BC，
∴④成立，⑤不成立；
∵∠D=∠BEC=90°，
∴∠DCE+∠DEC=∠DEC+∠AEB，
∴∠DCE=∠AEB，而∠D=∠A，
∴△DCE∽△AEB，
∴
| CD |
| AE |
| DE |
| AB |
| CE |
| DE |
| BE |
| AB |
∴①不成立，②、③成立，
故选B．
点评：该题主要考查了相似三角形的判定及其性质、勾股定理、射影定理等几何知识点及其应用问题；解题的关键是作辅助线，将分散的条件集中．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
对于反比例函数y=
，下列说法正确的是（ ）
| 1 |
| x |
| A、图象经过点（1，-1） |
| B、图象是中心对称图形 |
| C、图象位于第二、四象限 |
| D、当x＜0时，y随x的增大而增大 |
已知一粒米的质量是0.000019千克，科学记数法表示正确的是（ ）
| A、19×10-4千克 |
| B、1.9×10-6千克 |
| C、19×10-5千克 |
| D、1.9×10-5千克 |
如图，在△ABC中，∠BAC的平分线AB与BC交于点D，线段AD的垂直平分线与线段BC的延长线交于点F．若BD=3，CF=4，则CD=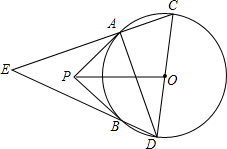
如图，PA，PB是⊙O的两条切线，切线分别是A，B．CD是⊙O的直径，直线AC，BD相交于点E．
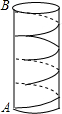为了庆祝“元旦”，学校准备在教学大厅的圆柱体柱子上贴彩带，已知柱子的底面周长为1m，高为3m．如果要求彩带从柱子底端的A处绕柱子1圈后到达柱子顶端的B处（线段AB与地面垂直），那么彩带的长度最短为
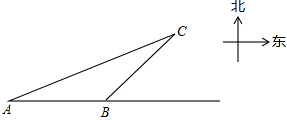一艘轮船自西向东航行，在A处测得东偏北30°方向有一座小岛C，继续向东航行60海里到达B处，测得小岛C此时在轮船的东偏北45°方向上．之后，轮船继续向东航行多少海里，距离小岛C最近？若2x=5y，则下列式子中正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|