题目内容
对于反比例函数y=
,下列说法正确的是( )
| 1 |
| x |
| A、图象经过点(1,-1) |
| B、图象是中心对称图形 |
| C、图象位于第二、四象限 |
| D、当x<0时,y随x的增大而增大 |
考点:反比例函数的性质
专题:
分析:根据反比例函数的性质对四个选项进行逐一分析即可.
解答:解:A、∵1×(-1)=-1≠1,∴点(1,-1)不在反比例函数y=
的图象上,故本选项错误;
B、反比例函数的图象关于原点中心对称,故本选项正确;
C、∵k=1>0,∴图象位于一、三象限,故本选项错误;
D、∵k=1>0,∴此函数在每一象限内y随x的增大而减小,故本选项错误.
故选B.
| 1 |
| x |
B、反比例函数的图象关于原点中心对称,故本选项正确;
C、∵k=1>0,∴图象位于一、三象限,故本选项错误;
D、∵k=1>0,∴此函数在每一象限内y随x的增大而减小,故本选项错误.
故选B.
点评:本题考查的是反比例函数的性质,熟知反比例函数的性质是解答此题的关键,即反比例函数的性质:
(1)反比例函数y=
(k≠0)的图象是双曲线;
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.
(1)反比例函数y=
| k |
| x |
(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;
(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.

练习册系列答案
相关题目
用配方法解方程x2-4x=1时,配方后变形正确的是( )
| A、(x-2)2=5 |
| B、(x-2)2=1 |
| C、(x-2)2=4 |
| D、(x-2)2=3 |
下列说法中正确的是( )
| A、x-1是单项式 | ||
B、
| ||
| C、-52x的系数是-5 | ||
D、
|
用四舍五入法要求对0.07019分别取近似值,其中错误的是( )
| A、0.1(精确到0.1) |
| B、0.07(精确到百分位) |
| C、0.07(精确到千分位) |
| D、0.0702(精确到0.0001) |
 求图中的字母A,B所代表的正方形的面积.
求图中的字母A,B所代表的正方形的面积. 如图,△ABC中,AD是角平分线,DE∥AC交AB于E,已知AB=12,AC=8,求DE.
如图,△ABC中,AD是角平分线,DE∥AC交AB于E,已知AB=12,AC=8,求DE. 尺规作图,不写作法,保留作图痕迹.
尺规作图,不写作法,保留作图痕迹.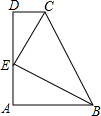 如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )
如图,CD∥AB,CE平分∠BCD,BE平分∠ABC,过点E作直线垂直CD于点D,交AB于点A,则下列关系式中成立的有( )