题目内容
16.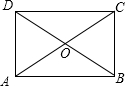 如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AD=3,则BD的长为6.
如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AD=3,则BD的长为6.
分析 由矩形的性质得出OA=OD,再证明△AOD是等边三角形,得出OD=AD=3,即可得出BD的长.
解答 解:∵四边形ABCD是矩形,
∴OA=$\frac{1}{2}$AC,OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OD,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴OD=AD=3,
∴BD=2OD=6;
故答案为:6.
点评 本题考查了矩形的性质、等边三角形的判定与性质;熟练掌握矩形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
11.已知平行四边形ABCD的周长为32,AB=4,则BC的长为( )
| A. | 4 | B. | 12 | C. | 24 | D. | 28 |
5.下列各式中,正确的是( )
| A. | $\sqrt{16}$=±4 | B. | -$\sqrt{16}$=4 | C. | $\root{3}{-8}$=-2 | D. | $\sqrt{(-4)^{2}}$=-4 |
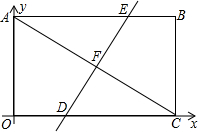 如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,
如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,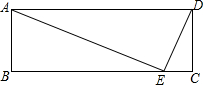 如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n,且m、n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2,试求BE的长.
如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n,且m、n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2,试求BE的长. 如图:
如图: