��Ŀ����
13����ƽ��ֱ������ϵ�У�������y=-$\frac{1}{2}$x2+tx+t+$\frac{1}{2}$��x�ύ��A��B���㣨��A�ڵ�B����� �����䶥��M��ֱ��y=2x�ϣ���1����t��ֵ��
��2����ͼ��CΪ�߶�OM��һ�㣬��C��x���ƽ���߽��߶�BM�ڵ�D����CDΪ��������������CDEF��CF��DE�ֱ���������P��Q���㣬�Ƿ���������ĵ�C��ʹ��������CDEF��������ܳ�ǡ�ñ�ֱ��PQƽ�֣������ڣ���C������ꣻ�������ڣ���˵�����ɣ�
��3������������A��B֮��IJ��֣�����A �͵�B������ƽ��n��n��0������λ��õ���ͼ���ΪG��ͬʱ��ֱy=4x+6����ƽ��n����λ������ͼ��ش�ƽ�ƺ��ֱ����ͼ��G�й�����ʱ��n��ȡֵ��Χ��
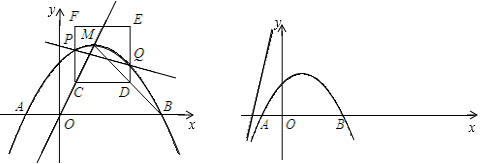
���� ��1�����ö��κ�������������϶���M��ֱ��y=2x�ϣ��ó�����t�ĵ�ʽ������ɣ�
��2���������ֱ��MB�Ľ���ʽ��������ʾ��E��F��P��Q�����꣬����������CDEF��������ܳ�ǡ�ñ�ֱ��PQƽ�֣���CP=EQ�����m��ֵ���ɣ�
��3�����ȼ���ƽ�ƺ��ֱ����ƽ�ƵĶ��κ������У���4x+6+n=-$\frac{1}{2}$��x-3+n����x+1+n����������ȵ�ʵ���������n��ֵ�������⣬������ƽ�ƺ��ֱ����ƽ�ƺ�������߲����У����ͼ���֪��ƽ�ƺ��ֱ����������G�����������㣬���������ٽ�Ľ���Ϊ����-n-1��0���루3-n��0���������ϵʽ������ɣ�
��� �⣺��1����y=-$\frac{1}{2}$x2+tx+t+$\frac{1}{2}$�ɵã�
x=-$\frac{b}{2a}$=t��y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{2��t+\frac{1}{2}��-{t}^{2}}{2}$��
�߶���M��ֱ��y=2x�ϣ�
��$\frac{2��t+\frac{1}{2}��-{t}^{2}}{2}$=2t��
��ã�t1=t2=1��
�������߽���ʽΪ��y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$��
��2����ͼ1����M��1��2����B��3��0������ֱ��MB�Ľ���ʽΪ��y=kx+d��
��$\left\{\begin{array}{l}{k+d=2}\\{3k+d=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-1}\\{d=3}\end{array}\right.$��
��ֱ��MB�Ľ���ʽΪ��y=-x+3��
��C��m��2m������D��3-2m��2m����
��������CDEF�ı߳�Ϊ��3-3m��
��E��3-2m��3-m����F��m��3-m����P��m��-$\frac{1}{2}$m2+m+$\frac{3}{2}$����Q��3-2m��-2m2+4m����
��������CDEF��������ܳ�ǡ�ñ�ֱ��PQƽ�֣�
��PQ�������ε����ģ�
��CP=EQ��
�ࣨ-$\frac{1}{2}$m2+m+$\frac{3}{2}$��-2m=��3-m��-��-2m2+4m����
�����ã�5m2-8m+3=0��
���ã�m1=$\frac{3}{5}$��m2=1����ȥ����
��C��$\frac{3}{5}$��$\frac{6}{5}$����
��3����ͼ2��������ɵã���B��C�䲿��ͼ��Ľ���ʽΪ��y=-$\frac{1}{2}$��x-3����x+1����-1��x��3��
������������ƽ�ƺ�õ���ͼ��G�Ľ���ʽΪ��
y=-$\frac{1}{2}$��x-3+n����x+1+n����-n-1��x��3-n��
��ʱֱ��ƽ�ƺ�Ľ���ʽΪ��y=4x+6+n��
���ƽ�ƺ��ֱ����ƽ�ƵĶ��κ������У�
��4x+6+n=-$\frac{1}{2}$��x-3+n����x+1+n����������ȵ�ʵ������
��-$\frac{1}{2}$x2-��n+3��x-$\frac{1}{2}$n2-$\frac{9}{2}$=0��������ȵ�ʵ������
�ʡ�=[-��n+3��]2-4����-$\frac{1}{2}$������-$\frac{1}{2}$n2-$\frac{9}{2}$��=6n=0��
��n=0��
������֪n��0��ì�ܣ�
��ƽ�ƺ��ֱ����ƽ�ƺ�������߲����У�
����ͼ���֪��ƽ�ƺ��ֱ����������G�����������㣬
���������ٽ�Ľ���Ϊ����-n-1��0���루3-n��0����
��0=4��-n-1��+6+n��
��ã�n=$\frac{2}{3}$��
0=4��3-n��+6+n��
��ã�n=6��
��n��ȡֵ��Χ�ǣ�$\frac{2}{3}$��n��6��
���� ������Ҫ�����˶��κ����ۺ��Լ������ε����ʺ�һԪ���η��̵ĸ����б�ʽ��֪ʶ���������μ��εó�ƽ�ƺ��ֱ����������G�������������ǽ���ؼ���

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д� �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�| A�� | y=-x | B�� | y=2+3x | C�� | y=5x | D�� | y=-3+2x |
| A�� | -6 | B�� | -12 | C�� | 12 | D�� | 27 |
| A�� | a=bcotB | B�� | a=csinA | C�� | $c=\frac{b}{cosA}$ | D�� | acosB=c |
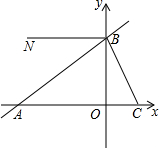 ��ͼ��������ϵ�У�ֱ��y=-3x+6��x��������ύ�ڵ�C����y��������ύ�ڵ�B��ֱ��BA��x��ĸ����ύ�ڵ�A��AB=5OC������BN��x�ᣮ
��ͼ��������ϵ�У�ֱ��y=-3x+6��x��������ύ�ڵ�C����y��������ύ�ڵ�B��ֱ��BA��x��ĸ����ύ�ڵ�A��AB=5OC������BN��x�ᣮ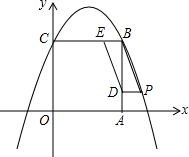 ��ͼ����ֱ������ϵxOy�У�������OABC�ı߳�Ϊ2cm����A��C�ֱ���x�ᡢy����������ϣ�������y=-x2+bx+c������B��C��
��ͼ����ֱ������ϵxOy�У�������OABC�ı߳�Ϊ2cm����A��C�ֱ���x�ᡢy����������ϣ�������y=-x2+bx+c������B��C��