题目内容
已知：在△ABC中，D为BC上一点，EG∥BC，分别交AB、AD、AC于点E、F、G，求证：AE：AF：AG=BE：DF：CG．考点：平行线分线段成比例
专题：证明题
分析：由平行可得
=
=
=k，则可得AE=kBE，AF=kFD，AG=kGC，则可得到结论．
| AE |
| BE |
| AF |
| FD |
| AG |
| GC |
解答：证明：∵EG∥BC，
∴
=
=
设
=
=
=k，则可得AE=kBE，AF=kFD，AG=kGC，
∴AE：AF：AG=kBE：kFD：kCG=BE：FD：CG．
∴
| AE |
| BE |
| AF |
| FD |
| AG |
| GC |
设
| AE |
| BE |
| AF |
| FD |
| AG |
| GC |
∴AE：AF：AG=kBE：kFD：kCG=BE：FD：CG．
点评：本题主要考查平行线分线段成比例，掌握平行线分线段中的线段对应成比例是解题的关键．注意参数法的应用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
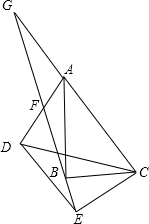如图，在△ABC和△DEC中，∠ABC=∠DEC=90°，连接AD交射线EB于F，过A作AG∥DE交射线EB于点G，点F恰好是AD中点．
如图示角度，CD=100m，求AB的高度？（精确到0.1m，
如图，在四边形ABCD中，AB∥CD，∠A=∠C=90°，AC=CD，AB=