题目内容
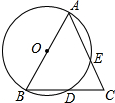如图，在△ABC中，AB=AC，∠BAC=50°，以AB为直径的圆分别交BC、AC于点D、E，则 |
| BD |
考点：圆周角定理,等腰三角形的性质
专题：
分析：连接OE，OD及AD，由AB为圆的直径，根据直径所对的圆周角为直角，AD与BC垂直，又AB=AC，根据三线合一得到AD为角平分线，由∠BAC的度数求出∠BAD及∠CAD的度数，再由同弧所对的圆心角等于所对圆周角的2倍，可得出圆心角∠BOD及∠DOE的度数，即可得到
的度数．
|
| BD |
解答：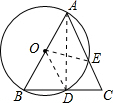
解：连接OE，OD，AD，
∵AB为圆O的直径，
∴∠ADB=90°，
又AB=AC，
∴AD为∠BAC的平分线，又∠BAC=50°，
∴∠BAD=∠CAD=25°，
又圆心角∠BOD与圆周角∠BAD都对
，
∴∠BOD=50，即
的度数为50°，
又圆心角∠EOD与圆周角∠CAD都对
，
∴∠DOE=50°，
∵∠BOD=50°，∠DOE=50°，
∴BD=DE，
∵BC=10cm，
∴BD=CD=5cm，
∴DE=5cm
故答案为50°，5．
解：连接OE，OD，AD，∵AB为圆O的直径，
∴∠ADB=90°，
又AB=AC，
∴AD为∠BAC的平分线，又∠BAC=50°，
∴∠BAD=∠CAD=25°，
又圆心角∠BOD与圆周角∠BAD都对
|
| BD |
∴∠BOD=50，即
|
| BD |
又圆心角∠EOD与圆周角∠CAD都对
|
| DE |
∴∠DOE=50°，
∵∠BOD=50°，∠DOE=50°，
∴BD=DE，
∵BC=10cm，
∴BD=CD=5cm，
∴DE=5cm
故答案为50°，5．
点评：本题考查了弦、弧及圆心角的关系，圆周角定理，以及等腰三角形的性质，其中连接出辅助线OD，OE及AD是解本题的关键．同时注意弧的度数即为弧所对圆心角的度数．
练习册系列答案
相关题目
如图，△ABC中，D是AB的黄金分割点（AD＜BD），过点D作DE∥BC交AC于E，若BC=3+
如图，在四边形ABCD中，AB∥CD，∠A=∠C=90°，AC=CD，AB=